Chapter 5
Field-Effect Transistors (FETs)
In this chapter we shall show how Spice is used to simulate circuits containing field-effect transistors (FETs). Spice has built-in models for two of the three FET types considered here, metal-oxide-semiconductor FETs (MOSFETs) and junction FETs (JFETs). In the case of metal-semiconductor FETs (MESFETs), we shall carry out our circuit simulations using the built-in model of PSpice. Various circuit examples involving the three types of FETs will be given.
5.1 Describing MOSFETs To Spice
MOSFETs are described to Spice using two statements; one statement describes the nature of the FET and its connections to the rest of the circuit, and the other specifies the values of the parameters of the built-in FET model. The following outlines the syntax of these two statements, including some details on the built-in ``Level 1'' MOSFET model of Spice.
|
Fig. 5.1: Spice element description for the NMOS and PMOS MOSFETs. Also listed is the general form of the associated MOSFET model statement. A partial listing of the parameter values applicable to either the NMOS or PMOS MOSFET is given in Table 5.1. Enhancement or depletion mode of operation is determined by the values assigned to these parameters.
|
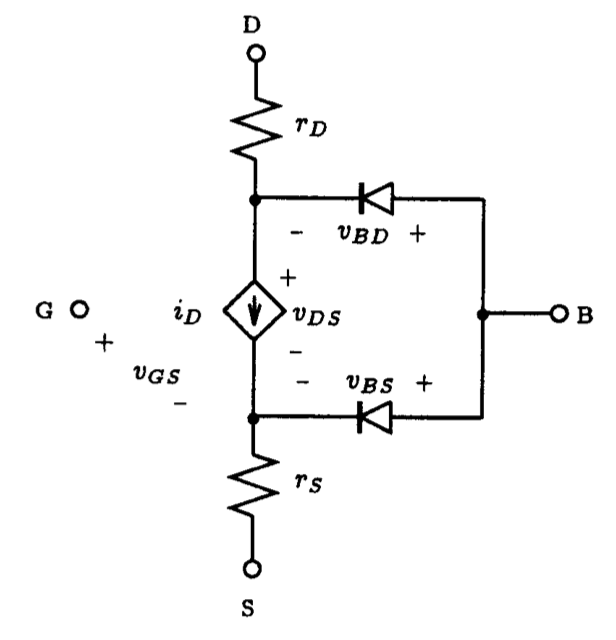
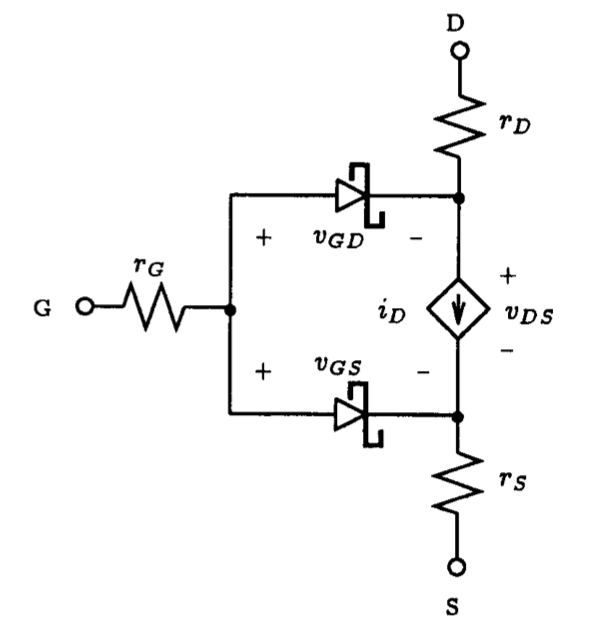
Fig. 5.2: The general form of the Spice large-signal model for an n-channel MOSFET under static conditions.
|
|
Table. 5.1: A partial listing of the Spice parameters for the LEVEL 1 MOSFET model.
|
5.1.1 MOSFET Element Description
The presence of a MOSFET in a circuit is described to Spice through the Spice input file using an element statement beginning with the letter M. If more than one MOSFET exists in a circuit, then a unique name must be attached to M to uniquely identify each transistor. This is then followed by a list of the nodes that the drain, gate, source, and substrate (body) of the MOSFET are connected to. Subsequently, on the same line, the name of the model that will be used to characterize a particular MOSFET is given. The name of this model must correspond to the name given on a model statement containing the parameter values that characterize this MOSFET to Spice. Finally, the length and width of the MOSFET are given. For quick reference, we depict in Fig. 5.1 the syntax for the Spice statement describing the MOSFET. Also listed is the syntax for the model statement (.MODEL) that must be present in any Spice input file that makes reference to the built-in MOSFET model of Spice. This statement specifies the terminal characteristics of the MOSFET by defining the values of particular parameters in the MOSFET model. Parameters of the model not specified are assigned default values by Spice. We shall briefly discuss the model statement next.
5.1.2 MOSFET Model Description
As is evident from Fig. 5.1, the model statement for either the NMOS or PMOS transistor begins with the keyword .MODEL and is followed by the name of the model used by a MOSFET element statement, the nature of the MOSFET (i.e., NMOS or PMOS), and a list giving the values of the model parameters (enclosed between brackets). The number of parameters associated with the Spice model of the MOSFET is large and their meaning complicated; besides, Spice has more than one large-signal model for the MOSFET. These are classified according to their levels of sophistication: Level 1, 2 and 3. The simplest MOSFET model being that described in Level 1. For the most part, MOSFET behavior described in Chapter 5 of Sedra and Smith is based on the Level 1 MOSFET model. The other two models are more complicated, and their mathematical description will not be discussed here. Rather, we shall just mention their important differences. The Level 2 MOSFET model is a more complex version of the LEVEL 1 model which includes extensive second-order effects, largely dependent on the geometry of the MOSFET. The Level 3 MOSFET model of Spice is a semi-empirical model (having some model parameters that are not necessarily physically based), especially suited to short-channel MOSFETs (i.e., L £ 5 um). For more details on these models, interested readers can consult reference [Vladimirescu, 1980].
Also, an advanced VLSI textbook by Geiger, Allen and Strader [Geiger, Allen and Strader, 1990] provides a good review of the three MOSFET models of Spice.
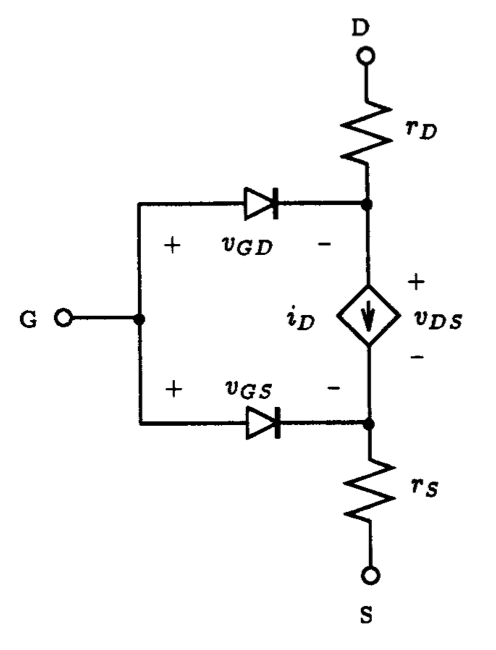
The general form of the DC Spice model for an n-channel MOSFET is illustrated schematically in Fig. 5.2. The bulk resistance of both the drain and source regions of the MOSFET are lumped into two linear resistances rD and rS, respectively. The DC characteristic of the intrinsic MOSFET is determined by the nonlinear dependent current source iD, and the two diodes represent the two substrate junctions that define the channel region. A similar model exists for the p-channel device; the direction of the diodes, the current source and the polarities of the terminal voltages are all reversed. The mathematical relationship that describes the DC behavior of the dependent current source varies depending on which level of model is used. For the LEVEL 1 MOSFET model, the expression for drain current iD, assuming that the drain is at a higher potential than the source, is described by the following[1]:

where the device constant K is related to process parameters and device geometry according to
(5.2)

and the threshold voltage Vt is given by
(5.3)
![]()
Here we see that the drain current equations are determined by the eight parameters: W, L, u, COX, Vt0, lambda, g and 2ff. Both W and L define the dimensions of the device. These two parameters are usually specified on the element statement of the MOSFET, although, if none is specified, Spice will assume that both W and L are 100 um. Parameters u and COX are process-related parameters that are multiplied together to form the process transconductance coefficient kp. It is kp that is usually specified in the parameter list of the model statement. The parameter Vt0 is the zero-bias threshold voltage. Vt0 is positive for enhancement-mode n-channel MOSFETs and depletion-mode p-channel MOSFETs. But, Vt0 is negative for depletion-mode n-channel MOSFETs and enhancement-mode p-channel MOSFETs. The parameter lambda is the channel-length modulation parameter and represents the influence that drain-source voltage has on the drain current iD when the device is in saturation. In Spice, the sign of this parameter is always positive, regardless of the nature of the device type. This is unlike the convention adopted by Sedra and Smith. The last two parameters, g and 2ff, are the body-effect parameter and the surface potential, respectively.
A partial listing of the parameters associated with the Spice MOSFET model under static conditions is given in Table 5.1. Also listed are default values which a parameter assumes if a value is not specified for it on the .MODEL statement. To specify a parameter value one simply writes, for example: level=1, kp=20u, Vto=1V, etc.
|
Fig. 5.3: A MOSFET circuit example.
|
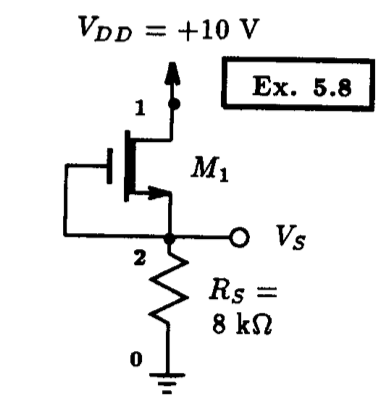
Example 5.1: Simple Enhancement-Mode MOSFET Circuit
** Circuit Description ** * dc supplies Vdd 1 0 DC +5V Vss 4 0 DC -5V * MOSFET circuit M1 2 0 3 3 nmos_enhancement_mosfet L=10u W=400u Rd 1 2 10k Rs 3 4 5k * mosfet model statement (by default, level 1) .model nmos_enhancement_mosfet nmos (kp=20u Vto=+2V lambda=0) ** Analysis Requests ** * calculate DC bias point .OP ** Output Requests ** * none required .end
Fig. 5.4: Spice input file for computing the DC operating point of the circuit shown in Fig. 5.3.
|
5.1.3 An Enhancement-Mode N-Channel MOSFET Circuit
In the following we shall calculate the DC conditions of a circuit containing a FET using Spice. Both the DC node voltages of the circuit and the DC operating point information of the FET will be determined.
Consider the circuit shown in Fig. 5.3, the particulars of this design were presented in Example 5.1 of Sedra and Smith, 3rd Edition. Here we would like to confirm that the FET is indeed biased at a current level of 0.4 mA and that the voltage appearing at the drain is +1 V. The NMOS transistor is assumed to have Vt=2 V, unCOX= 20 uA/V2, L=10 um, and W=400 um. Furthermore, the channel-length modulation effect is assumed zero (i.e., lambda=0). Assuming a level 1 MOSFET model, we can create the following Spice model statement for this FET using the above information as:
.model nmos_enhancement_mosfet nmos (kp=20u Vto=+2V lambda=0)
Here, we have labeled the name of this model as: nmos_enhancement_mosfet. The meaning behind this name should be obvious. Transistor M1, and its geometry, is then described to Spice using the following element statement:
M1 2 0 3 3 nmos_enhancement_mosfet L=10u W=400u
where we have assumed that the substrate (body) is connected to the source. Combining these statements with the ones for the other devices of the circuit shown in Fig. 5.3, results in the Spice input file shown in Fig. 5.4. Submitting this file with an operating point (.OP) analysis request to Spice, results in the following DC circuit information:
|
**** SMALL SIGNAL BIAS SOLUTION TEMPERATURE = 27.000 DEG C ****************************************************************************
NODE VOLTAGE NODE VOLTAGE NODE VOLTAGE NODE VOLTAGE
( 1) 5.0000 ( 2) 1.0000 ( 3) -3.0000 ( 4) -5.0000
VOLTAGE SOURCE CURRENTS NAME CURRENT
Vdd -4.000E-04 Vss 4.000E-04
TOTAL POWER DISSIPATION 4.00E-03 WATTS
**** OPERATING POINT INFORMATION TEMPERATURE = 27.000 DEG C ****************************************************************************
**** MOSFETS
NAME M1 MODEL nmos_enhancement_mosfet ID 4.00E-04 VGS 3.00E+00 VDS 4.00E+00 VBS 0.00E+00 VTH 2.00E+00 VDSAT 1.00E+00
|
As expected, these results confirm that the FET is biased at the intended current level of 0.4 mA, and also that the drain of the FET is at the correct voltage level of +1 V. As a further note, we see from the above results that M1 is biased in its saturation region because vDS > VDS,SAT where Spice uses the notation VDS,SAT= VGS - Vt.
|
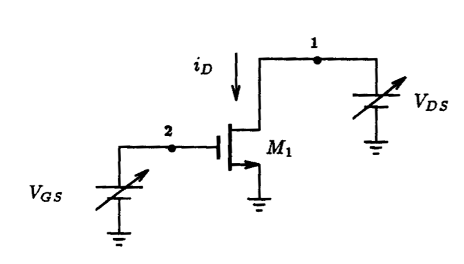
Fig. 5.5: Spice curve-tracer arrangement for calculating the i - v characteristics of a MOSFET. The iD - vDS characteristic of the MOSFET is obtained by sweeping vDS through a range of voltages while keeping VGS constant at some value. The iD - VGS characteristic of the MOSFET is obtained by sweeping VGS through a range of values while vDS is held constant.
|
Enhancement-Mode N-Channel MOSFET Id - Vds Characteristics
** Circuit Description ** * bias conditions Vds 1 0 DC +10V ; this value is arbitrary, we are going to sweep it Vgs 2 0 DC +3V * MOSFET under test M1 1 2 0 0 nmos_enhancement_mosfet L=10u W=400u * mosfet model statement (by default, level 1) .model nmos_enhancement_mosfet nmos (kp=20u Vto=+2 lambda=0) ** Analysis Requests ** .DC Vds 0V 10V 100mV ** Output Requests ** .Plot DC I(Vds) V(1) .Probe .end
Fig. 5.6: The Spice input file for computing the iD - vDS characteristic of a MOSFET with device parameters: Vt=+2 V, un COX= 20 uA/V2, lambda=0 V-1, L=10 um, and W=400 um. The gate-source voltage VGS is set equal to +3 V and the drain-source voltage is swept between 0 and +10 V in 100 mV increments.
|

Fig. 5.7: Comparing the iD - vDS characteristics of a MOSFET with a channel-width modulation factor lambda=0 and lambda=0.05 V-1. The gate-source voltage is held constant at +3 V.
5.1.4 Observing the MOSFET Current - Voltage Characteristics
The iD - vDS characteristics of a MOSFET are easily obtained by sweeping the drain-to-source voltage through a range of DC voltages, all the meanwhile, the gate-to-source voltage is held constant at some voltage value. The drain current of the MOSFET is then monitored and plotted against the drain-source voltage. To demonstrate how one performs this operation on a MOSFET using Spice, consider the circuit shown in Fig. 5.5. Here two independent voltage sources, VGS and vDS, will be used to establish the different bias conditions on the enhancement-mode n-channel MOSFET whose source and body are connected together. It is assumed that the MOSFET has the same geometry and device parameters that were previously mentioned in the last subsection. Repeating them here, the NMOS transistor is characterized by Vt=+2 V, unCOX= 20 uA/V2, L=10 um, and W=400 um. The modulation factor will be assumed equal to zero, i.e., lambda=0 V-1. Let us consider setting VGS=+3 V and sweep vDS from 0 V to +10 V in steps of 100 mV. In this way, the MOSFET will be taken through both its triode and saturation regions of operation. The resulting drain current is then monitored by observing the current supplied by voltage source vDS. The Spice input file representing this situation is listed in Fig. 5.6.
The results of this analysis are shown plotted in Fig. 5.7 as the curve marked by lambda=0. Here the behavior of the MOSFET is as expected from Eqn. (5.1): For drain-source voltages less than VDS,SAT, (VDS,SAT=VGS-Vt=+1 V), the MOSFET is in its triode region. For drain-source voltages above +1 V, the MOSFET saturates at a current level of 400 uA. The slope of the line drawn tangent to the output current in the saturation region is 0. Thus, the incremental drain-source resistance is infinite. It is interesting to compare the iDS - vDS characteristic of a similar MOSFET having a nonzero channel-length modulation coefficient. For the case of an identical MOSFET but with lambda=0.05 V-1, the iDS - vDS curve is shown superimposed on the same graph as that in Fig. 5.7. This curve was obtained with results calculated with the same Spice deck seen previously in Fig. 5.6, except with the MOSFET model statement modified according to:
.model nmos_enhancement_mosfet nmos (kp=20u Vto=+2V lambda=0.05).
On comparison, we see that the effect of a nonzero channel-length modulation coefficient results in an output current that increases with increasing drain-source voltage at a rate of 20.314 uA/V. Thus, the corresponding incremental drain-source resistance is 49.23 kW. It is re-assuring that this increment resistance agrees quite closely with the value estimated by hand analysis; e.g., for a drain current of approximately 400 uA, ro which is given by 1/(lambdaID), is estimated to be 50 kW.
Another current - voltage characteristic that is used to describe the behavior of a MOSFET is: iD versus VGS. The circuit arrangement illustrated in Fig. 5.5 can also be used to obtain this current - voltage behavior. Instead of varying the drain-source voltage, this voltage is held constant and the gate-source voltage of the MOSFET is swept over a desired range. To demonstrate this, consider setting vDS to +5 V and sweeping VGS from 0 V to +5 V in increments of 100 mV. The Spice deck describing this is very similar to that used previously and is seen listed in Fig. 5.8. Here we have modeled the MOSFET like before with the channel-modulation coefficient set to zero. For comparison, we have created another Spice file that is identical to that seen in Fig. 5.8 except with the MOSFET having a channel-modulation coefficient lambda=0.05 V-1. These two Spice decks are then concatenated together and submitted to Spice for analysis.
The results of these two Spice analyses are shown in Fig. 5.9. Here we have plotted the iD - VGS curves for the two cases of lambda=0 and lambda=0.05 V-1. As is evident, the presence of a nonzero lambda gives rise to a vertical shift in drain current. One interpretation of this is that for a given gate-source voltage, a MOSFET with non-zero channel-length modulation will draw more current from a circuit than one with zero channel-length modulation.
|
Fig. 5.5: Spice curve-tracer arrangement for calculating the i - v characteristics of a MOSFET. The iD - vDS characteristic of the MOSFET is obtained by sweeping vDS through a range of voltages while keeping VGS constant at some value. The iD - VGS characteristic of the MOSFET is obtained by sweeping VGS through a range of values while vDS is held constant.
(Duplicate)
|
Enhancement-Mode N-Channel MOSFET Id - Vgs Characteristics
** Circuit Description ** * bias conditions Vds 1 0 DC +5V Vgs 2 0 DC +3V ; this value is arbitrary, we are going to sweep it * MOSFET under test M1 1 2 0 0 nmos_enhancement_mosfet L=10u W=400u * mosfet model statement (by default, level 1) .model nmos_enhancement_mosfet nmos (kp=20u Vto=+2 lambda=0) ** Analysis Requests ** .DC Vgs 0V 10V 100mV ** Output Requests ** .Plot DC I(Vgs) V(2) .Probe .end
Fig. 5.8: The Spice input file for computing the iD - VGS characteristic of a MOSFET with device parameters: Vt=+2 V, un COX= 20 uA/V2, lambda=0 V-1, L=10 um, and W=400 um. The drain-source voltage vDS is set equal to +5 V and the gate-source voltage is swept between 0 and +5 V in 100 mV increments. The drain-source voltage is held constant at +5 V. |

Fig. 5.9: Comparing the iD - VGS characteristics of a MOSFET with a channel-length modulation factor lambda=0 and lambda=0.05 V-1. The drain-source voltage is held constant at +5 V.
5.2 Spice Analysis of MOSFET Circuits At DC
MOSFETs are classified as n-channel or p-channel devices depending on the material used to form the channel. In addition, these devices are classified according to their mode of operation as enhancement or depletion type devices. As a result, the model statement characterizing these different FETs have subtle differences. In the following we shall highlight these differences as we analyze the DC operating point of several simple MOSFET circuits contained within Chapter 5 of Sedra and Smith, 3rd Edition. Our results can then be compared with those derived by hand analysis in Sedra and Smith.
5.2.1 An Enhancement-Mode P-Channel MOSFET Circuit
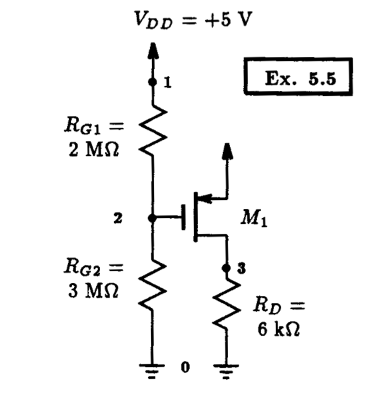
Consider the circuit shown in Fig. 5.10. Here we have a single transistor circuit containing a p-channel enhancement-mode MOSFET. The resistors have been chosen such that the FET is biased in its saturation region, has a bias current of 0.5 mA, and a drain voltage of +3 V. It is also assumed that the MOSFET has a threshold voltage of -1 V, a process transconductance parameter upCOX equal to 1 mA/V2 and does not exhibit any channel-length modulation effect (i.e., lambda=0). The details of this design can be found in Example 5.5 of Sedra and Smith, 3rd Edition.
|
Fig. 5.10: A transistor circuit designed in Example 5.5 of Sedra and Smith. Spice is used to calculate the DC operating point of this circuit.
|
Example 5.5: A Simple Enhancement-Mode PMOS Circuit (Rd=6k)
** Circuit Description ** * dc supplies Vdd 1 0 DC +5V * MOSFET circuit M1 3 2 1 1 pmos_enhancement_mosfet L=10u W=10u Rd 3 0 6k Rg1 1 2 2Meg Rg2 2 0 3Meg * mosfet model statement (by default, level 1) .model pmos_enhancement_mosfet pmos (kp=1m Vto=-1V lambda=0) ** Analysis Requests ** * calculate DC bias point .OP ** Output Requests ** * none required .end
Fig. 5.11: Spice input file for calculating the DC operating point of the p-channel MOSFET circuit shown in Fig. 5.10.
|
This circuit would be described to Spice in the usual way; however, because the dimensions of the MOSFET are not given we shall assume arbitrarily that the length and width of it are both equal to 10 um. The model statement describing the characteristics of the p-channel MOSFET would appear as follows:
.model pmos_enhancement_mosfet pmos (kp=1m Vto=-1V lambda=0)
Here we have declared the MOSFET to be a PMOS device, and by assigning a negative threshold voltage, we are indicating to Spice that this particular PMOS device is of the enhancement-mode.
The Spice input deck for this particular example is listed in Fig. 5.11. We are requesting that Spice compute the DC operating point of this circuit. The results of this analysis are then found in the output file and some of its contents are on display below:
|
**** SMALL SIGNAL BIAS SOLUTION TEMPERATURE = 27.000 DEG C ****************************************************************************
NODE VOLTAGE NODE VOLTAGE NODE VOLTAGE NODE VOLTAGE
( 1) 5.0000 ( 2) 3.0000 ( 3) 3.0000
VOLTAGE SOURCE CURRENTS NAME CURRENT
Vdd -5.010E-04
TOTAL POWER DISSIPATION 2.51E-03 WATTS
**** OPERATING POINT INFORMATION TEMPERATURE = 27.000 DEG C ****************************************************************************
**** MOSFETS
NAME M1 MODEL pmos_enhancement_mosfet ID -5.00E-04 VGS -2.00E+00 VDS -2.00E+00 VBS 0.00E+00 VTH -1.00E+00 VDSAT -1.00E+00
|
As is evident from above, the p-channel MOSFET is biased at a current level of 0.5 mA and that its drain is at +3 V. The sign of ID is negative because of the convention adopted by Spice; positive drain current flows into the drain terminal of a FET regardless of the device type. This is different than the convention used in Sedra and Smith. One should be aware of this convention difference. We also know that the device is biased in its saturation region because vDS < VDS,SAT. It is interesting to note that if we alter the value of RD from 6 kW to 8 kW, and re-run the Spice input file, then we find that M1 is biased on the edge of saturation (i.e., vDS=VDS,SAT). This is evident from the results found in the Spice output file as follows:
|
**** SMALL SIGNAL BIAS SOLUTION TEMPERATURE = 27.000 DEG C ****************************************************************************
NODE VOLTAGE NODE VOLTAGE NODE VOLTAGE NODE VOLTAGE
( 1) 5.0000 ( 2) 3.0000 ( 3) 4.0000
VOLTAGE SOURCE CURRENTS NAME CURRENT
Vdd -5.010E-04
TOTAL POWER DISSIPATION 2.51E-03 WATTS
**** OPERATING POINT INFORMATION TEMPERATURE = 27.000 DEG C ****************************************************************************
**** MOSFETS
NAME M1 MODEL pmos_enhancement_mosfet ID -5.00E-04 VGS -2.00E+00 VDS -1.00E+00 VBS 0.00E+00 VTH -1.00E+00 VDSAT -1.00E+00
|
Any increase in RD above 8 kW will certainly cause M1 to move out of the saturation region and into the triode region.
5.2.2 A Depletion-Mode P-Channel MOSFET Circuit
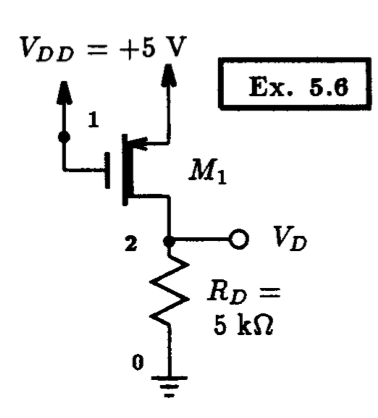
An example of a circuit incorporating a depletion-mode p-channel MOSFET is illustrated in Fig. 5.12. The depletion mode PMOS transistor is assumed to have Vt=+1 V, upCOX=1 mA/V2 and lambda=0. With Spice, we would like to compute the drain current and the corresponding drain voltage. The Spice input file for this particular circuit is listed in Fig. 5.13. Take note of the model statement describing the depletion mode PMOS transistor, which we repeat below for convenience:
.model pmos_depletion_mosfet pmos (kp=1m Vto=+1V lambda=0)
In contrast to the enhancement mode PMOS transistor of the last example, the threshold voltage for a depletion mode PMOS transistor is made positive but everything else remains the same.
|
Fig. 5.12: A depletion-mode p-channel MOSEFT circuit.
|
Example 5.6: A Depletion-Mode PMOS Transistor Circuit
** Circuit Description ** * dc supplies Vdd 1 0 DC +5V * MOSFET circuit M1 2 1 1 1 pmos_depletion_mosfet L=10u W=10u Rd 2 0 5k * mosfet model statement (by default, level 1) .model pmos_depletion_mosfet pmos (kp=1m Vto=+1V lambda=0) ** Analysis Requests ** * calculate DC bias point .OP ** Output Requests ** * none required .end
Fig. 5.13: Spice input file for calculating the DC operating point of the depletion-mode p-channel MOSFET circuit shown in Fig. 5.12.
|
Submitting the input file to Spice, results in the following DC bias information:
|
**** SMALL SIGNAL BIAS SOLUTION TEMPERATURE = 27.000 DEG C ****************************************************************************
NODE VOLTAGE NODE VOLTAGE NODE VOLTAGE NODE VOLTAGE
( 1) 5.0000 ( 2) 2.5000
VOLTAGE SOURCE CURRENTS NAME CURRENT
Vdd -5.000E-04
TOTAL POWER DISSIPATION 2.50E-03 WATTS
**** OPERATING POINT INFORMATION TEMPERATURE = 27.000 DEG C ****************************************************************************
**** MOSFETS
NAME M1 MODEL pmos_depletion_mosfet ID -5.00E-04 VGS 0.00E+00 VDS -2.50E+00 VBS 0.00E+00 VTH 1.00E+00 VDSAT -1.00E+00
|
Thus, the drain current and voltage of transistor M1 are 0.5 mA and +2.5 V, respectively. Also, we see that the transistor is operating in the saturation region (i.e., vDS < VDS,SAT). These results are identical to those computed by hand in Example 5.6 of Sedra and Smith, 3rd Editon.
In the above analysis, the effect of channel-length modulation was assumed zero. In practise, this is not the case. In the following we repeat the above analysis assuming the transistor has a more realistic channel-length modulation coefficient of lambda=0.02 V-1. We shall then compare the resulting transistor drain current with that obtained previously. This will give us some sense of how practical the assumption of neglecting the effect of channel-length modulation is when computing the DC bias point of a MOSFET circuit.
To carry out this task, we simply change the transistor model statement seen previously in Fig. 5.13 to the following:
.model pmos_depletion_mosfet pmos (kp=1m Vto=+1V lambda=0.02)
and re-submit the Spice deck for analysis. The results of the analysis are then found in the Spice output file. The pertinent details are shown below:
|
**** SMALL SIGNAL BIAS SOLUTION TEMPERATURE = 27.000 DEG C ******************************************************************************
NODE VOLTAGE NODE VOLTAGE NODE VOLTAGE NODE VOLTAGE
( 1) 5.0000 ( 2) 2.6190
VOLTAGE SOURCE CURRENTS NAME CURRENT
Vdd -5.238E-04
TOTAL POWER DISSIPATION 2.62E-03 WATTS
**** OPERATING POINT INFORMATION TEMPERATURE = 27.000 DEG C ******************************************************************************
**** MOSFETS
NAME M1 MODEL pmos_depletion_mosfet ID -5.24E-04 VGS 0.00E+00 VDS -2.38E+00 VBS 0.00E+00 VTH 1.00E+00 VDSAT -1.00E+00
|
Thus, we see that the transistor drain current is now 524 uA as a result of the channel-modulation effect. This is about a 5% increase in the transistor drain current of 500 uA when no channel-length modulation effect was present. When performing ``back-of-the-envelop'' type calculations, neglecting the channel-length modulation effect seems to be quite reasonable. When more accuracy is required, one resorts to the use of Spice.
5.2.3 A Depletion-Mode N-Channel MOSFET Circuit
As the final example of this section, we shall look at a circuit containing a depletion-mode NMOS transistor. Consider the circuit shown in Fig. 5.14 where M1 is assumed to have the following parameters: Vt=-1 V, un COX=1 mA/V2}, and lambda=0. A Spice listing of this particular circuit is compiled in Fig. 5.15 and the results of an operating point analysis (.OP) are presented, in part, below:
|
Fig. 5.14: A depletion-mode n-channel MOSFET circuit.
|
Example 5.8: A Depletion-Mode NMOS Transistor Circuit
** Circuit Description ** * dc supplies Vdd 1 0 DC +10V * MOSFET circuit M1 1 2 2 2 nmos_depletion_mosfet L=10u W=10u Rd 2 0 100k * mosfet model statement (by default, level 1) .model nmos_depletion_mosfet nmos (kp=1m Vto=-1V lambda=0) ** Analysis Requests ** * calculate DC bias point .OP ** Output Requests ** * none required .end
Fig. 5.15: The Spice input file for calculating the DC operating point of the depletion-mode n-channel MOSFET circuit shown in Fig. 5.14.
|
|
**** SMALL SIGNAL BIAS SOLUTION TEMPERATURE = 27.000 DEG C ****************************************************************************
NODE VOLTAGE NODE VOLTAGE NODE VOLTAGE NODE VOLTAGE
( 1) 10.0000 ( 2) 9.8956
VOLTAGE SOURCE CURRENTS NAME CURRENT
Vdd -9.896E-05
TOTAL POWER DISSIPATION 9.90E-04 WATTS
**** OPERATING POINT INFORMATION TEMPERATURE = 27.000 DEG C ****************************************************************************
**** MOSFETS
NAME M1 MODEL nmos_depletion_mosfet ID 9.90E-05 VGS 0.00E+00 VDS 1.04E-01 VBS 0.00E+00 VTH -1.00E+00 VDSAT 1.00E+00
|
Notice that in this case vDS < VDS,SAT, implying that the transistor is operating in the triode region.
In the following, we repeat the above analysis with the same MOSFET model used above with the addition that it has a channel-length modulation coefficient lambda equal to 0.04 V-1. On doing so, we find in the Spice output file the following DC operating information:
|
**** SMALL SIGNAL BIAS SOLUTION TEMPERATURE = 27.000 DEG C ******************************************************************************
NODE VOLTAGE NODE VOLTAGE NODE VOLTAGE NODE VOLTAGE
( 1) 10.0000 ( 2) 9.8960
VOLTAGE SOURCE CURRENTS NAME CURRENT
Vdd -9.896E-05
TOTAL POWER DISSIPATION 9.90E-04 WATTS
**** OPERATING POINT INFORMATION TEMPERATURE = 27.000 DEG C ******************************************************************************
**** MOSFETS
NAME M1 MODEL nmos_depletion_mosfet ID 9.90E-05 VGS 0.00E+00 VDS 1.04E-01 VBS 0.00E+00 VTH -1.00E+00 VDSAT 1.00E+00
|
Thus, we see that only the voltage at the second (2) node has changed to 9.8960 V from the previous value of 9.8956 V. All other values listed appear to be the same as before; given the 3 or 4 digits of accuracy. Thus, the inclusion of the term (1 + lambdavDS) does not seem to affect the behavior of the circuit significantly when the device is operated in the triode region.
5.3 Describing JFETs To Spice
Like MOSFETs, JFETs are described to Spice using an element statement and a model statement. The following outlines the syntax of these two statements, including the details of the built-in JFET model.

Fig. 5.16: Spice element description for the n-channel and p-channel JFETs. Also listed is the general form of the JFET model statement. A partial listing of the parameters applicable to either an n-channel or p-channel JFET is given in Table 5.2.
5.3.1 JFET Element Description
JFETs are describe to Spice using an element statement beginning with a unique name prefixed with the letter J. This is then followed by a list of the nodes that the drain, gate, and source of the JFET are connected to. The next field specifies the name of the model that characterizes its terminal behavior, and the final field of this statement is optional, and its purpose is to allow one to scale the size of the device by specifying the number of JFETs connected in parallel. A summary of the element statement syntax for both the n-channel and p-channel JFETs is provided in Fig. 5.16. Included in this list is the syntax for the JFET model statement (.MODEL). This statement defines the terminal characteristics of the JFET by specifying the values of parameters in the JFET model. Parameters not specified in the model statement are assigned default values by Spice. Details of this model will be discussed briefly next.
|
Fig. 5.17: The Spice large-signal n-channel JFET model under static conditions.
|
Table. 5.2: A partial listing of the Spice parameters for the JFET model.
|
5.3.2 JFET Model Description
As is evident from Fig. 5.16, the model statement for either the n-channel or p-channel JFET transistor begins with the keyword .MODEL and is followed by the name of the model used by a JFET element statement, the nature of the JFET (i.e., NJF or PJF), and a list of the JFET parameter values (enclosed between brackets). Specifically, the mathematical model of the JFET in Spice is very similar to that seen earlier for the Level 1 MOSFET model.
The general form of the DC Spice model for an n-channel JFET is illustrated schematically in Fig. 5.17. The bulk resistance of the drain and source regions of the JFET are lumped into two linear resistances rD and rS, respectively. The DC characteristic of the intrinsic JFET is determined by the nonlinear dependent current source iD, and the two diodes represent the two substrate junctions that define the channel region. A similar model applies for the p-channel device; the direction of the diodes, the current source and the polarities of the terminal voltages are all reversed. The expression for drain current iD, assuming that the drain is at a higher potential than the source, is described by the following:
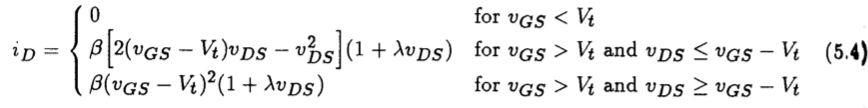
where the device parameters b and Vt are written in terms of IDSS and VP as
(5.5)
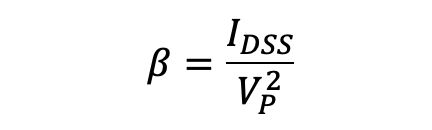
and
(5.6)
![]()
From the above, we see that the JFET has 3 parameters that define its operation: IDSS, VP and lambda. The parameter IDSS is the drain current when VGS=0 V, and VP corresponds to the pinch-off voltage of the channel. The parameter lambda is the channel-length modulation parameter and represents the influence that the drain-source voltage has on the drain current iD when the device is in pinch-off. The sign of this parameter is always positive, regardless of the nature of the device type. A note on notation: The transconductance coefficient b is denoted by the parameter K in Sedra and Smith.
A partial listing of the parameters associated with the Spice JFET model under static conditions is given in Table 5.2. Also listed are the default values which the parameter assume if no value is specified on the .MODEL statement. To specify a parameter value one simply writes, for example: beta=1m, Vto=-1V, lambda=0.01, etc.
|
Fig. 5.18: An n-channel JFET circuit example.
|
Example 5.9: A Simple N-Channel JFET Circuit
** Circuit Description ** * dc supplies Vdd 1 0 DC +10V * JFET circuit J1 2 0 3 n_jfet Rd 1 2 1k Rs 3 0 0.5k * n-channel jfet model statement .model n_jfet NJF (beta=1m Vto=-4V lambda=0) ** Analysis Requests ** * calculate DC bias point .OP ** Output Requests ** * none required .end
Fig. 5.19: The Spice input file for calculating the DC operating point of the JFET circuit shown in Fig. 5.18.
|
5.3.3 An N-Channel JFET Example
To demonstrate how a circuit containing a JFET is described to Spice, consider the circuit shown in Fig. 5.18. Here the JFET is n-channel with parameters: VP=-4 V, IDSS=16 mA and lambda=0. The model statement for this particular n-channel JFET that would appear in the Spice input file is as follows:
.model n_jfet NJF (beta=1m Vto=-4V lambda=0)
In this particular case, one had to convert the device parameters into terms that Spice is familiar with. This required that one compute b from IDSS and VP according to b = IDSS/VP2. Vt is simply equal to VP.
In keeping with the discussion thus far, we shall compute the DC operating point of the circuit shown in Fig. 5.18. The Spice input file for this circuit, including the appropriate analysis request (i.e., .OP command), is listed in Fig. 5.19. On completion of Spice, the following results are found in the output file:
|
**** SMALL SIGNAL BIAS SOLUTION TEMPERATURE = 27.000 DEG C ****************************************************************************
NODE VOLTAGE NODE VOLTAGE NODE VOLTAGE NODE VOLTAGE
( 1) 10.0000 ( 2) 6.0000 ( 3) 2.0000
VOLTAGE SOURCE CURRENTS NAME CURRENT
Vdd -4.000E-03
TOTAL POWER DISSIPATION 4.00E-02 WATTS
**** OPERATING POINT INFORMATION TEMPERATURE = 27.000 DEG C ****************************************************************************
**** JFETS
NAME J1 MODEL n_jfet ID 4.00E-03 VGS -2.00E+00 VDS 4.00E+00
|
Here we see that the JFET is biased with a drain current of 4 mA and that the drain is at a voltage of 6 V.
|
Fig. 5.20: A p-channel JFET circuit.
|
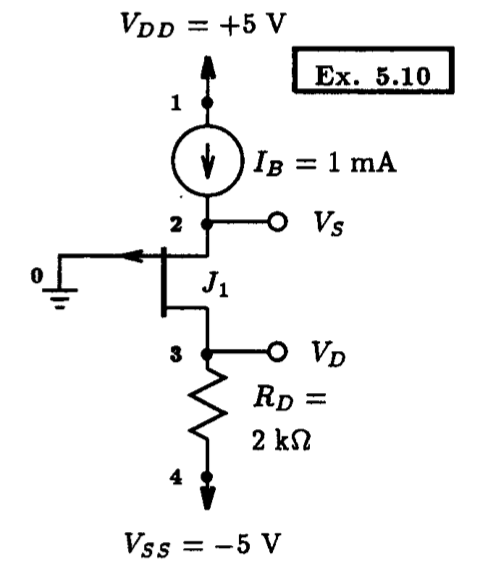
Example 5.10: A Simple P-Channel JFET Circuit
** Circuit Description ** * dc supplies Vdd 1 0 DC +5V Vss 4 0 DC -5V Ib 1 2 DC 1mA * JFET circuit J1 3 0 2 p_jfet Rd 3 4 2k * p-channel jfet model statement .model p_jfet PJF (beta=1m Vto=-2V lambda=0) ** Analysis Requests ** * calculate DC bias point .OP ** Output Requests ** * none required .end
Fig. 5.21: The Spice input file for calculating the DC operating point of the p-channel JFET circuit shown in Fig. 5.20.
|
5.3.4 A P-Channel JFET Example
This next example is along the same lines as the previous JFET example except that the JFET is p-channel. The p-channel JFET circuit that we will analyze for its DC bias conditions is on display in Fig. 5.20. Here the p-channel device has parameters: VP=+2 V, IDSS=4 mA and lambda=0. The importance of this example is to highlight the fact that the threshold voltage (Vt) of the p-channel JFET is specified on the model statement as a negative value, even though VP is positive. One must be careful of this for it is opposite to what is used in Sedra and Smith. The rationale for this is that the originators of Spice adopted the convention that a depletion-mode device, which the JFET is, would have Vt < 0 whether it be n-channel or p-channel.
The Spice input file describing the circuit shown in Fig. 5.20 is listed below in Fig. 5.21. On completion of Spice, the following results are found in the output file:
|
**** SMALL SIGNAL BIAS SOLUTION TEMPERATURE = 27.000 DEG C ****************************************************************************
NODE VOLTAGE NODE VOLTAGE NODE VOLTAGE NODE VOLTAGE
( 1) 5.0000 ( 2) -1.0000 ( 3) -3.0000 ( 4) -5.0000
VOLTAGE SOURCE CURRENTS NAME CURRENT
Vdd -1.000E-03 Vss 1.000E-03
TOTAL POWER DISSIPATION 1.00E-02 WATTS
**** OPERATING POINT INFORMATION TEMPERATURE = 27.000 DEG C ****************************************************************************
**** JFETS
NAME J1 MODEL p_jfet ID -1.00E-03 VGS 1.00E+00 VDS -2.00E+00
|
As is evident, the transistor is biased at 1 mA, and the source and drain are at -1 V and -3 V, respectively.
To see how much the DC bias calculation changes with the inclusion of the transistor channel-length modulation effect, we repeat the above analysis with lambda=0.04 V-1. Modifying the Spice deck shown listed in Fig. 5.21 to reflect this change, we then submit the revised Spice deck to Spice. The following results are then obtained:
|
**** SMALL SIGNAL BIAS SOLUTION TEMPERATURE = 27.000 DEG C ******************************************************************************
NODE VOLTAGE NODE VOLTAGE NODE VOLTAGE NODE VOLTAGE
( 1) 5.0000 ( 2) -1.0371 ( 3) -3.0000 ( 4) -5.0000
VOLTAGE SOURCE CURRENTS NAME CURRENT
Vdd -1.000E-03 Vss 1.000E-03
TOTAL POWER DISSIPATION 1.00E-02 WATTS
**** OPERATING POINT INFORMATION TEMPERATURE = 27.000 DEG C ******************************************************************************
**** JFETS
NAME J1 MODEL p_jfet ID -1.00E-03 VGS 1.04E+00 VDS -1.96E+00
|
Since the JFET is biased externally with a current source the effect of the channel-length modulation will manifest itself in the voltages that appear across the terminals of the device. For instance, the gate-source voltage increases from 1 V to 1.04 V. Likewise, the drain-source voltage experiences the same voltage change. In both cases, the resulting voltage change is small, and this provides further justification that it is reasonable to neglect the presence of channel-length modulation when performing DC bias calculations by hand.
5.4 FET Amplifier Circuits
Field-effect transistors are commonly employed in the design of linear amplifiers. Small-signal linear analysis is commonly employed as a means of estimating various attributes of amplifier behavior when subjected to small input signals. Examples of amplifier attributes would include input and output resistances, and current and voltage signal gain. Spice has a small-signal linear model of the MOSFET and another for the JFET. We shall describe these in this section. Subsequently, we shall illustrate the effectiveness of small-signal analysis as it applies to a common-source n-channel enhancement-mode MOSFET amplifier. This is accomplished by comparing the results calculated by the formulae presented in Sedra and Smith with those generated by Spice. But before these undertakings, we shall illustrate the importance of biasing a FET around an operating point that is well within the saturation region of the device.
|
Fig. 5.22: A fixed-bias n-channel MOSFET amplifier configuration.
|
An Enhancement-Type NMOS Amplifier
** Circuit Description ** * dc supplies Vdd 1 0 DC +20V Vgs 4 0 DC +5V * small-signal input vi 3 4 PWL (0,0 0.25ms,+0.5V 0.75ms,-0.5V 1.25ms,+0.5V 1.75ms,-0.5V + 2.25ms,+0.5V 2.75ms,-0.5V 3ms,0V) * amplifier circuit M1 2 3 0 0 nmos_enhancement_mosfet L=10u W=10u Rd 1 2 1.33k * mosfet model statement (by default, level 1) .model nmos_enhancement_mosfet nmos (kp=2m Vto=+2V) ** Analysis Requests ** .OP .TRAN 10us 3ms 0ms 10us ** Output Requests ** .PLOT TRAN V(2) V(3) .probe .end
Fig. 5.24: The Spice input file for calculating the large-signal transient behavior of the MOSFET amplifier shown in Fig. 5.22 with a drain resistor of 1.33 kW.
|
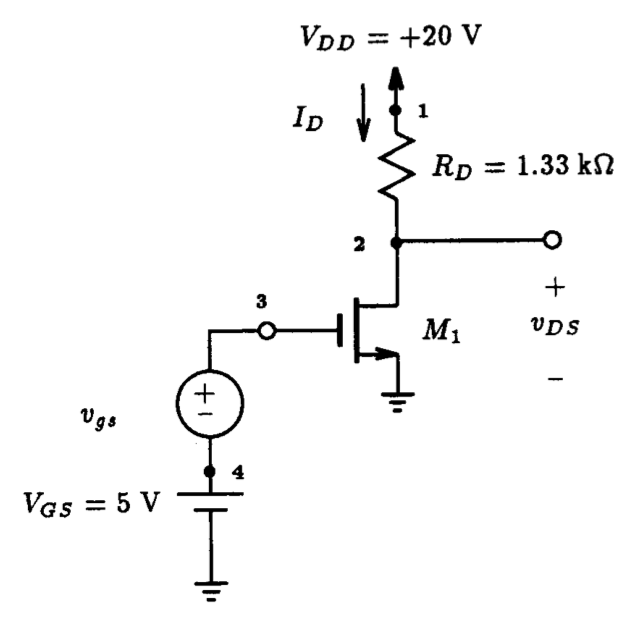
5.4.1 Effect of Bias Point on Amplifier Conditions
In this section we consider the effect that a misplaced DC operating point has on the large-signal operation of a MOSFET amplifier. For the enhancement-type n-channel MOSFET amplifier shown in Fig. 5.22 with a +5 V fixed-biasing scheme, the DC operating point of the MOSFET has been set at approximately ID=9 mA and vDS=8 V. This is a result of the MOSFET having an assumed threshold voltage Vt of +2 V, a conductance parameter K= 1/2xunCOX(W/L)=1 mA/V2 and a channel-length modulation factor lambda=0.01 V-1.
Figure 5.23 shows the iD - vDS characteristics for this device obtained using the curve tracer method described in Section 5.1. Also shown superimposed on this graph is the 1.33 kW load line. We see that the resulting operating point Q1 is located slightly to the left of the midway point between the triode and cut-off regions. If the drain resistance RD is increase to 1.78 kW, then the DC operating point, Q2, located at ID=9.3 mA and vDS=3.6 V, moves closer to the edge of the triode region.
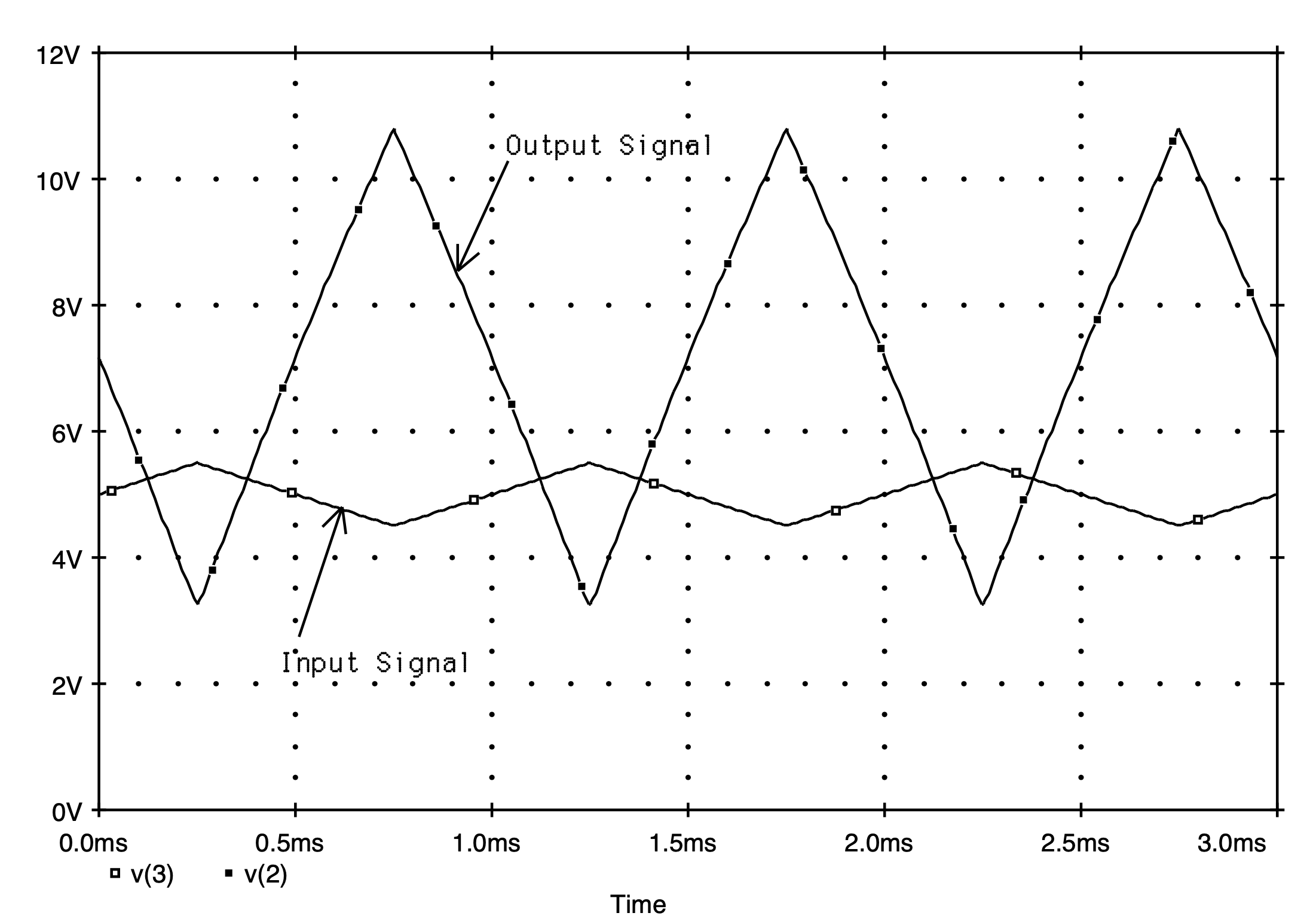
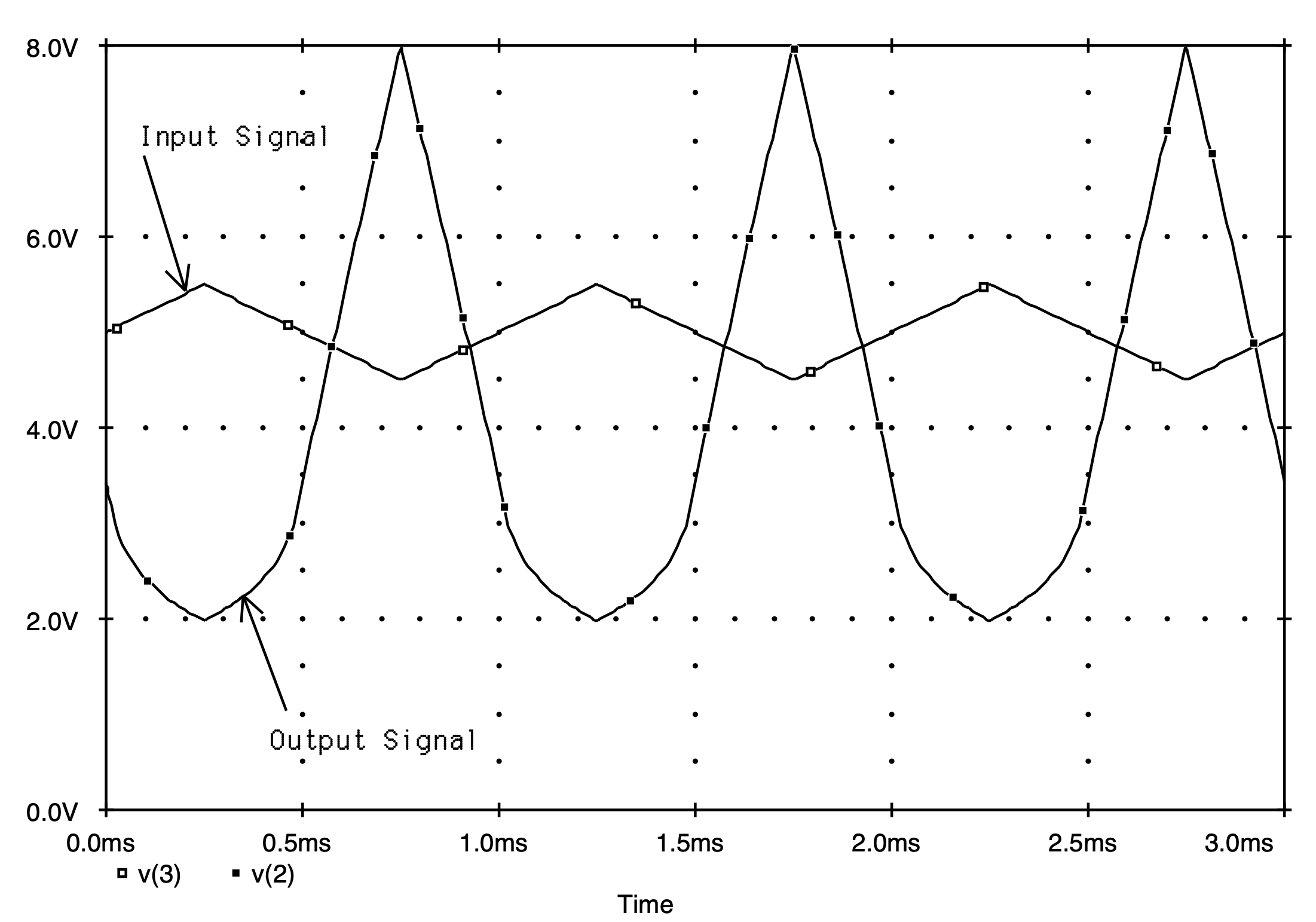
To illustrate the effect that the location of the DC operating point has on the large-signal behavior of the amplifier, consider applying a 1 V peak-to-peak triangular waveform input signal of 1 kHz frequency in series with the 5 V DC biasing voltage as shown in Fig. 5.22. This will then be repeated for the same amplifier having a drain resistance of 1.78 kW, and the resulting output signals from each amplifier will be compared. The Spice input file describing the first situation is provided in Fig. 5.24. Here the triangular input is described using the piecewise linear source statement for a time duration of 3 ms. A transient analysis command is included to compute the behavior of this amplifier over the same time period.
The results of the two Spice analyses are shown in Fig. 5.25. The top graph in part (a) of this figure illustrates both the input and output waveforms for a drain resistance of 1.33 kW. As is evident the output signal is reasonably linear with a peak-to-peak level about 8 times that of the input signal (more precisely, 7.53 times). This is in contrast with the case when the drain resistance is increased to 1.78 kW where we see in Fig. 5.23(b) that the output signal has become quite distorted in the lower portion of its waveform. Thus, this example helps to illustrate the importance of placing the DC operating point of an amplifier well within the saturation region of the MOSFET in order to maximize the output voltage swing of the amplifier while maintaining linear operation.
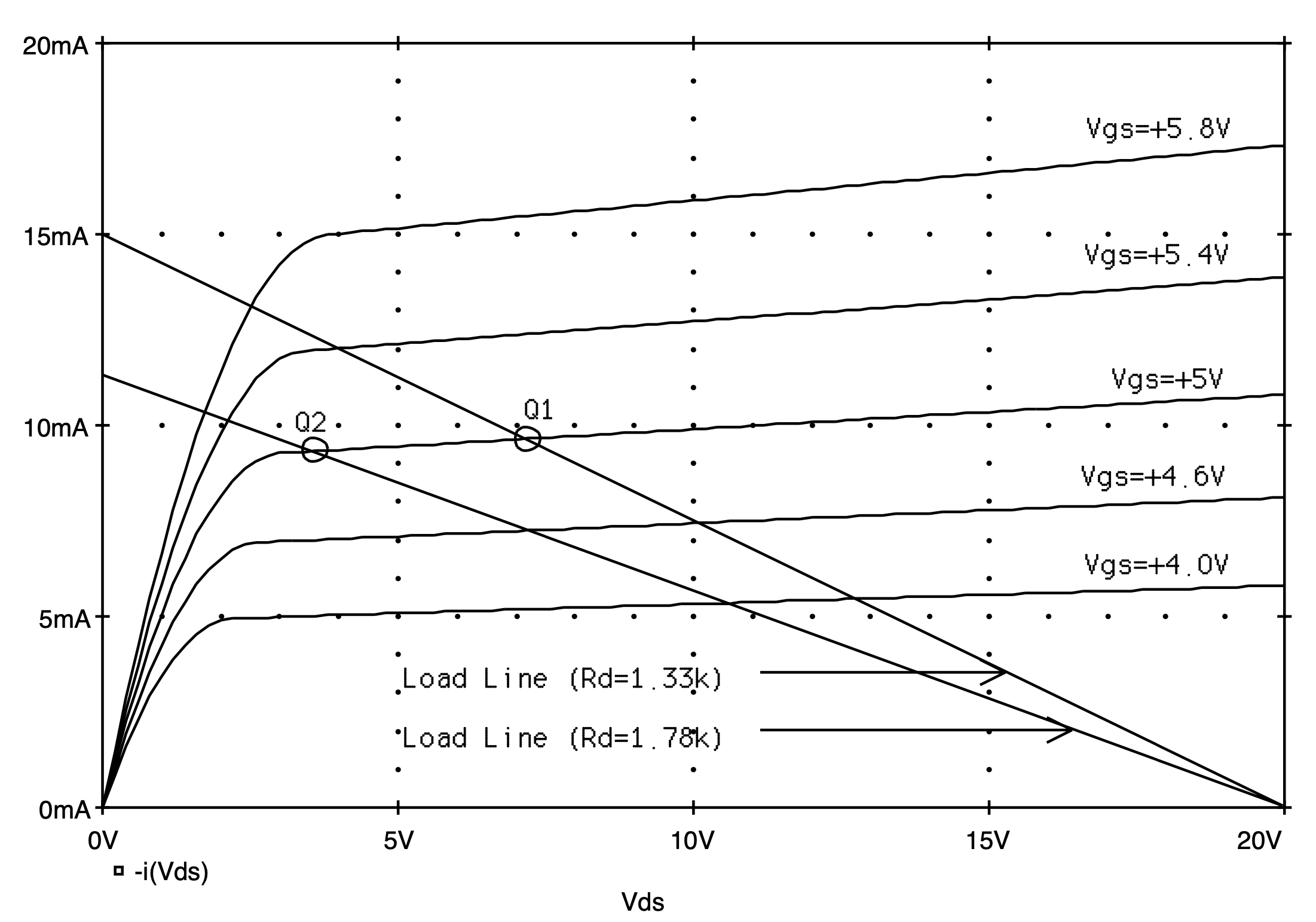
Fig. 5.23: The iD-vDS characteristics of an n-channel MOSFET having model parameters Vt=+2 V, 1/2unCOX(W/L)=1 mA/V2 and lambda=0.01 V-1. Load lines for the MOSFET amplifier shown in Fig. 5.22 for drain resistances of 1.33 kW and 1.78 kW. Q1 and Q2 indicate the DC operating point of each amplifier with a gate-source bias voltage of 5 V.
|
(a) |
(b) |
|
|
|
Fig. 5.25: The input and output large-signal transient behavior of the MOSFET amplifier shown in Fig. 5.22 for a drain resistance of: (a) 1.33 kW (b) 1.78 kW.
|
(a) |
(b) |
|
|
|
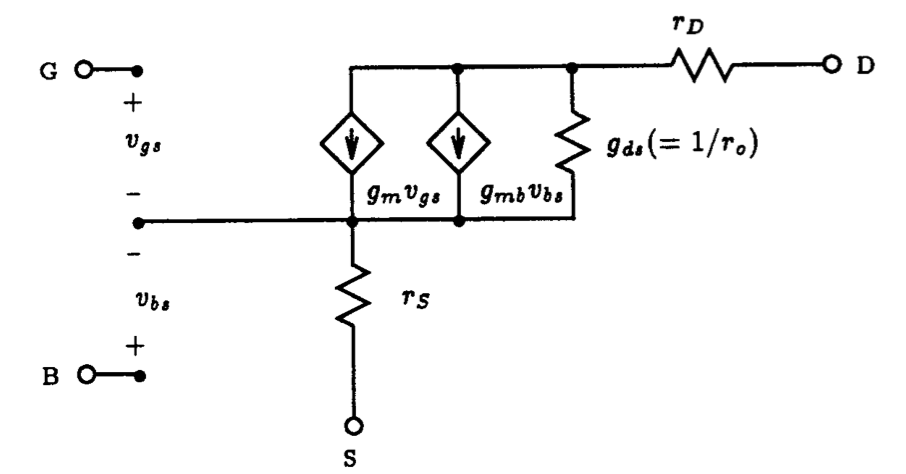
Fig. 5.26: The static Spice small-signal model of: (a) MOSFET, (b) JFET.
5.4.1 Small-Signal Model of the FET
The linearized small-signal model for the MOSFET is shown in Fig. 5.26(a). It consists of two voltage-controlled current sources with transconductance gm and gmb. The MOSFET transconductance, gm, is related to the DC bias current ID and the device parameters (ignoring the channel-length modulation effect) as follows:
(5.7)
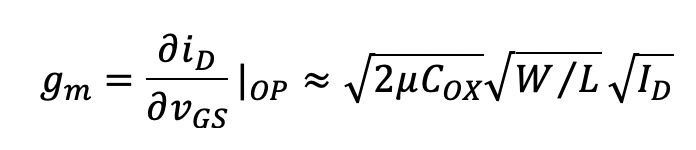
Here |OP indicates that the derivative is obtained at the DC operating point of the device. The next term, gmb, is known as the body transconductance and is related to several MOSFET bias conditions and device parameters according to:
(5.8)
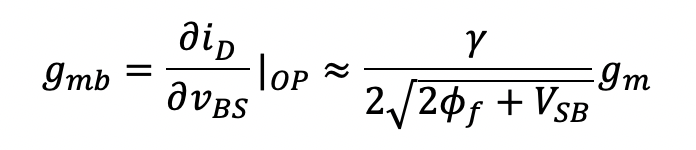
Accounting for the presence of channel-length modulation, the output conductance gds, which is also equal to 1/ro, is given approximately by the expression
(5.9)

Finally, the resistances rD and rS represent the ohmic resistance of drain and source regions, respectively. The small-signal linear model of a JFET is shown in Fig. 5.26(b). It consists of a single voltage-controlled current source having a transconductance gm that is related to the DC bias current ID and device parameters (ignoring the channel-length modulation effect) according to the following:
(5.10)
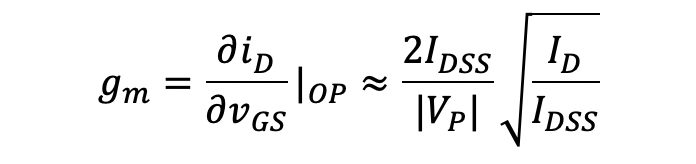
Accounting for the presence of channel-length modulation, the output conductance gds, which is also equal to 1/ro, is given approximately by the expression
(5.11)

Lastly, the resistances rD and rS represent the ohmic resistance of the drain and source regions, respectively.
Many of the analysis that is performed on a transistor circuit by Spice utilizes its linear small-signal equivalent circuit. The parameters of the small-signal model of each transistor in a given circuit, as computed by Spice, are available to the user through the operating point (.OP) command. To see this, consider a single NMOS transistor with its drain biased at +5 V, its gate biased at +3 V, and its source connected to ground. Furthermore, we shall assume that the substrate is biased at -5 V. The transistor is assumed to have the following parameters: Vt0=+1 V, unCOX= 20 uA/V2, L=10 um, and W=400 um. Furthermore, lambda=0.05 V-1 and g=0.9 V1/2. The Spice input file for this circuit is provided below:
|
Small-Signal Model Of An N-Channel MOSFET
** Circuit Description ** * mosfet terminal bias Vd 1 0 DC +5V Vg 2 0 DC +3V Vb 3 0 DC -5V * mosfet under test M1 1 2 0 3 nmos_enhancement_mosfet L=10u W=400u * mosfet model statement (by default, level 1) .model nmos_enhancement_mosfet nmos (kp=20u Vto=1V lambda=0.05 gamma=0.9) ** Analysis Requests ** .OP ** Output Requests ** * none required .end
|
On completion of Spice, one finds in the Spice output file the following complete list of parameters pertaining to the small-signal MOSFET model computed by Spice:
|
**** OPERATING POINT INFORMATION TEMPERATURE = 27.000 DEG C
**** MOSFETS
NAME M1 MODEL nmos_enhancement_mosfet ID 1.61E-04 VGS 3.00E+00 VDS 5.00E+00 VBS -5.00E+00 VTH 2.43E+00 VDSAT 5.67E-01 GM 5.67E-04 GDS 6.44E-06 GMB 1.08E-04 CBD 0.00E+00 CBS 0.00E+00 CGSOV 0.00E+00 CGDOV 0.00E+00 CGBOV 0.00E+00 CGS 0.00E+00 CGD 0.00E+00 CGB 0.00E+00
|
Included in the above list of operating point information are: (a) DC bias conditions which include drain current and various terminal voltages; (b) device transconductances gm and gmb; (c) output conductance gds; and (d) device capacitances accounting for MOSFET dynamic effects. All the parameters in this list, except for the capacitances (these are all zero for the time being), have been discussed previously and therefore their meaning should be self-evident. A discussion of MOSFET capacitances will be deferred until Chapter 7.
Similar results extend to the JFET. We leave this to the reader to confirm.
|
Fig. 5.27: A common-source amplifier circuit.
|
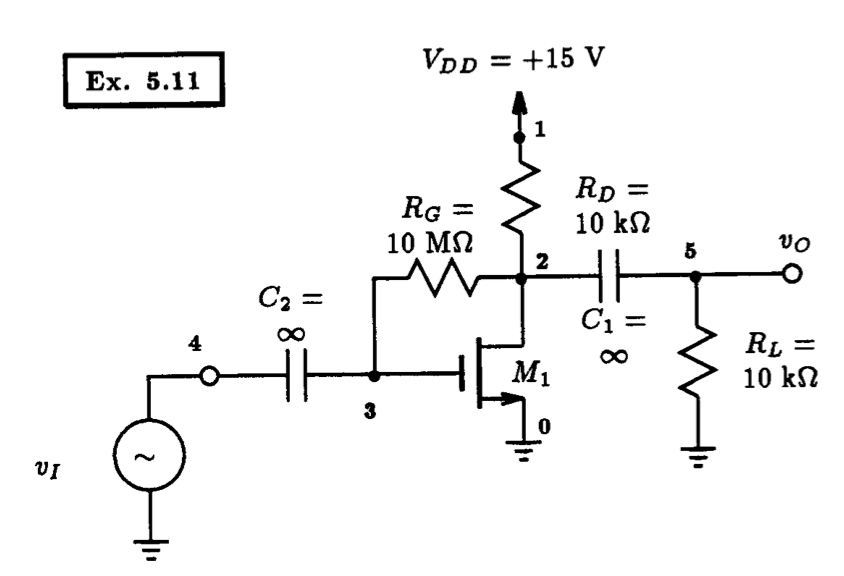
Example 5.11: An Enhancement-Mode NMOS Amplifier
** Circuit Description ** * dc supplies Vdd 1 0 DC +15V * input AC signal Vi 4 0 DC 0V * amplifier circuit M1 2 3 0 0 nmos_enhancement_mosfet L=10u W=10u Rd 1 2 10k Rg 2 3 10Meg C1 2 5 1GF C2 3 4 1GF * load Rl 5 0 10k * mosfet model statement (by default, level 1) .model nmos_enhancement_mosfet nmos (kp=0.25m Vto=+1.5V lambda=0.02) ** Analysis Requests ** .OP ** Output Requests ** * node required .end
Fig. 5.28: The Spice input file for calculating the DC operating point and small-signal model parameters of the amplifier circuit shown in Fig. 5.27.
|
5.4.2 A Basic FET Amplifier Circuit
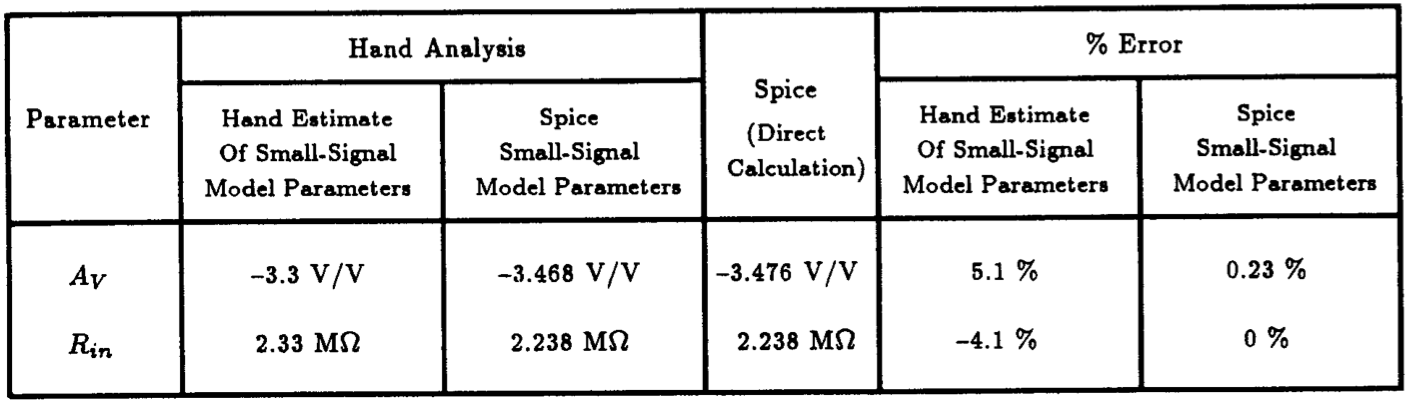
Fig. 5.27 displays an enhancement-mode NMOS amplifier in which the input signal vI is coupled to the gate of the MOSFET through a large capacitor, and the output signal at the drain is coupled to the load resistance R_L via another large capacitor. The MOSFET is assumed to have device parameters: Vt=+1.5 V, uCOX=0.5 mA/V2} and lambda=0.02 V-1. This same example was analyzed by hand in Example 5.11 of Sedra and Smith, 3rd Edition. There they found that this amplifier would have a voltage gain of -3.3 V/V and an input resistance of 2.33 MW. These results were obtained by performing a small-signal analysis of the amplifier circuit through a two-step procedure. The first step was to obtain the DC bias conditions of the circuit, specifically the drain current, from which the small-signal model for the transistor is obtained. The second step was to analyze the linear small-signal equivalent circuit of the amplifier to obtain the voltage gain and the input resistance. In each step of the analysis some simplifying assumptions are made. For instance, during the DC bias calculation, the transistor channel-length modulation effect was ignored. In the second step, a simplifying assumption was made with regards to the current flowing through the feedback resistor RG. We have seen in previous examples of this chapter that ignoring the channel-length modulation effect results in small variations in the drain current of a MOSFET, and thus, by extension, variations in the small-signal model parameters would also be small. In the following, with the aid of Spice, we would like to investigate the accuracy of these two steps as they apply to the common-source amplifier in Fig. 5.27 and demonstrate that these simplifying assumptions are reasonable.
According to the hand analysis performed in Example 5.11 of Sedra and Smith (which ignores the channel-length modulation effect) the drain current of the MOSFET is found to be 1.06 mA. Thus, from Eqns. (5.7) and (5.11) the MOSFET transconductance gm equals 0.725 mA/V and the output resistance ro is equal to 47 kW. To compare these results to those calculated by Spice, we have created the Spice input file listed in Fig. 5.28. The infinite-valued coupling capacitors are represented by 1 giga-farads. This will ensure that the capacitors behave as short circuits at the signal frequencies of interest. The results generated by Spice are as follows:
|
**** MOSFETS
NAME M1 MODEL nmos_enhancement_mosfet ID 1.07E-03 VGS 4.31E+00 VDS 4.31E+00 VBS 0.00E+00 VTH 1.50E+00 VDSAT 2.81E+00 GM 7.62E-04 GDS 1.97E-05 GMB 0.00E+00
|
Here we see that the MOSFET is biased at a drain current of 1.07 mA, has a transconductance gm equal to 0.762 mA/V and an output conductance of 19.7 uS, or an output resistance ro of 50.8 kW. Comparing the hand calculated values of Sedra and Smith with those generated by Spice, we see that the hand calculated results are quite close, with at most, a 7.5% error. In Table 5.3 we list these two sets of results and also list the relative error between them.
|
Table. 5.3: Comparing the transistor drain current ID and its corresponding small-signal model parameters gm and ro as computed by straightforward hand analysis and Spice. |
Once the small-signal equivalent circuit of the amplifier is obtained, one proceeds to analyze the circuit using standard circuit analysis techniques to obtain pertinent amplifier parameters, such as voltage gain and input resistance. To gain insight into circuit behavior, closed-form expressions are usually derived from the equivalent circuit. In many cases, the expressions that result are complicated, large, and not very insightful. As a result, one makes simplifying assumptions based on practical considerations that lead to expressions that are simpler, but more insightful. For example, in Example 5.11 of Sedra and Smith, 3rd Edition, the linear small-signal equivalent circuit of the common-source amplifier shown in Fig. 5.27 was analyzed and the following expressions for its voltage gain and input resistance were obtained after making several practical assumptions:
(5.12)
![]()
and
(5.13)

It is the simplicity of these two formulas that makes them useful in circuit design. The question then becomes: How accurate are they?
To verify their accuracy, we simply substitute the appropriate circuit parameters, together with the small-signal parameters of the MOSFET generated by Spice above and evaluate. This is then compared with the results computed directly by Spice. For the first part, we find AV=-3.468 V/V and Rin=2.238 kW. With regard to the analysis we ask Spice to perform, one might be tempted to request a transfer function (.TF) analysis and directly obtain both the small-signal voltage gain and the amplifier input resistance. Unfortunately, the amplifier is AC coupled and intended to amplify signals containing frequencies other than DC. Since the .TF analysis calculates the small-signal input - output behavior of a circuit only at DC, in the situation at hand the results produced would not prove very useful. Instead, we shall apply a one-volt AC voltage signal to the input of the amplifier and compute the voltage appearing at the amplifier output using the .AC analysis command of Spice at a single midband frequency of, say, 1 Hz. A one-volt input level is usually chosen here because, in this way, the output voltage would be directly equal to the input - output transfer function. The input signal level of one-volt is not considered to be above the small-signal limit of the amplifier because the .AC analysis performed by Spice is performed directly with the small-signal equivalent circuit of the amplifier. Thus, any input level would work. The Spice statements necessary to invoke this analysis are as follows:
Vi 4 0 AC 1V
.AC LIN 1 1Hz 1Hz
In a similar vein, we can compute the input resistance of amplifier by determining the current that is supplied by the input voltage source and computing the input resistance as the ratio of the input voltage to input current. To obtain this information, we ask Spice to print both the magnitude and phase of the output voltage signal (node 5), followed by the magnitude and phase of the current supplied by Vi, using the following Spice statement:
.PRINT AC Vm(5) Vp(5) Im(Vi) Ip(Vi)
Recall that Spice uses complex variables to evaluate the AC small-signal response of a circuit, so one must indicate the form of the complex variable (i.e., magnitude, real, imaginary, etc.) you want Spice to print.
The AC analysis results computed by Spice at 1 Hz would then be found in the output file as follows:
|
**** AC ANALYSIS TEMPERATURE = 27.000 DEG C
FREQ VM(5) VP(5) IM(Vi) IP(Vi)
1.000E+00 3.467E+00 -1.800E+02 4.467E-07 1.800E+02
|
The small-signal voltage gain of the amplifier (AV) is therefore -3.476 V/V and the input resistance Rin is 2.238 MW (=1/4.467 x 10-7 MW). The phase of the input current IP(Vi) indicates that the sign of the current supplied by the input voltage source Vi is negative. This is consistent with the convention used by Spice; that is, current supplied by a source to a circuit is always negative.
|
Table. 5.4: Comparing the voltage gain and the input resistance of the amplifier shown in Fig. 5.27 as calculated by three different methods: (a) closed-form expression using hand estimates of the small-signal model parameters; (b) closed-form expression using Spice calculated small-signal model parameters; (c) direct calculation using Spice.
|
Comparing these two sets of results, one set derived using hand analysis together with Spice generated small-signal model parameters (-3.468 V/V, 2.238 MW), and the other derived directly using Spice (-3.476 V/V, 2.238 MW), we see that these results are either identical to one another or quite close with a relative error of only 0.23%. We can therefore conclude that the simplifying assumptions used to derive the formula for small-signal voltage gain and input resistance in Sedra and Smith are very reasonable and introduce very little error. When the small-signal parameters computed by hand are used instead of the Spice generated model parameters, the accuracy of the results decrease but remain within practical limits (i.e., AV=-3.3 V/V and Rin=2.33 MW). The relative error of the two calculations are in the vicinity of 5%. This error is largely due to the error incurred through the DC hand analysis which ignored the transistor channel-length modulation effect. A summary of the above discussion is provided in Table 5.4 for easy reference.
|
|
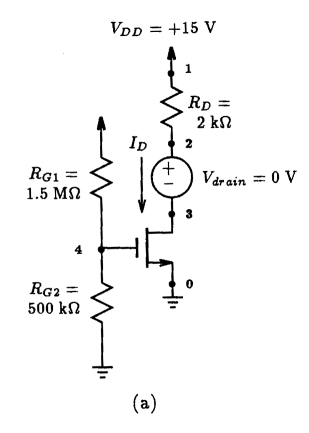
Simple MOSFET Bias Network (No Feedback Mechanism)
** Circuit Description ** * dc supply Vdd 1 0 DC +15V * amplifier circuit M1 3 4 0 0 nmos L=100u W=100u Rg1 1 4 1.5Meg Rg2 4 0 500k Rd 1 2 2k * drain current monitor Vdrain 2 3 0 * mosfet model statement (by default, level 1) .model nmos nmos (kp=2m Vto=+2V lambda=0) ** Analysis Requests ** .OP .SENS I(Vdrain) ** Output Requests ** .end
Fig. 5.30: The Spice input file for calculating the DC sensitivities of the drain current of the MOSFET amplifier shown in Fig. 5.29(a).
|
|
Fig. 5.29: Two different MOSFET biasing arrangements: (a) fixed biasing (b) biasing with source resistance feedback. The zero-valued voltage source in series with the drain terminal of each MOSFET is used to directly monitor the drain current.
|
MOSFET Bias Network With Feedback
** Circuit Description ** * dc supply Vdd 1 0 DC +15V * amplifier circuit M1 3 4 5 0 nmos L=100u W=100u Rg1 1 4 1Meg Rg2 4 0 2Meg Rd 1 2 2k Rs 5 0 2.2k * drain current monitor Vdrain 2 3 0 * mosfet model statement (by default, level 1) .model nmos nmos (kp=2m Vto=+2V lambda=0) ** Analysis Requests ** .OP .SENS I(Vdrain) ** Output Requests ** .end
Fig. 5.31: The Spice input file for calculating the DC sensitivities of the drain current of the MOSFET amplifier shown in Fig. 5.29(b).
|
5.5 Investigating Bias Stability with Spice
To obtain a stable DC operating point in discrete transistor circuits, a biasing scheme utilizing some form of negative feedback is usually employed. This ensures that the DC bias currents through the transistors in the circuit remain relatively constant under the influence of normal manufacturing or environmental variations.
To illustrate the effectiveness of incorporating negative feedback in the biasing network of a transistor amplifier, let us compare the DC sensitivities of the two amplifiers shown in Fig. 5.29 to the resistive biasing components. Each MOSFET will be assumed to have the following parameters: Vt=+2 V and unCOX=2 mA/V2. For a fair comparison, each amplifier is biased at approximately the same current level of 3 mA. The n-channel enhancement MOSFET amplifier of Fig. 5.29(a) is simply biased by a voltage appearing at its gate terminal. Although, the MOSFET in the amplifier of Fig. 5.29(b) is also biased with a voltage at its gate through a voltage divider circuit, a resistor is included in the source lead of the MOSFET which provides a feedback action that acts to stabilize the drain current of the MOSFET when subjected to change. What this means is, if one of the biasing elements undergoes a small change, then the resulting drain current of the MOSFET will experience less change than when no feedback action is present. To see this, we created the two Spice input files listed in Figs. 5.30 and 5.31 with the following sensitivity analysis request:
.SENS I(Vdrain)
This command will invoke Spice to compute the DC sensitivities of the drain current of each MOSFET as monitored by the zero-valued voltage source that appears in series with its drain terminal. The sensitivity analysis command of Spice was first introduced to the reader in Section 4.5 of this text.
The results of this analysis, as found in the Spice output file, are shown below for the amplifier circuit of Fig. 5.29(a). First, we show the bias conditions of the amplifier, followed by a list of the circuit DC sensitivities.
|
**** OPERATING POINT INFORMATION TEMPERATURE = 27.000 DEG C
**** MOSFETS
NAME M1 MODEL nmos ID 3.06E-03 VGS 3.75E+00 VDS 8.88E+00 VBS 0.00E+00 VTH 2.00E+00 VDSAT 1.75E+00
**** DC SENSITIVITY ANALYSIS TEMPERATURE = 27.000 DEG C
DC SENSITIVITIES OF OUTPUT I(Vdrain)
ELEMENT ELEMENT ELEMENT NORMALIZED NAME VALUE SENSITIVITY SENSITIVITY (AMPS/UNIT) (AMPS/PERCENT)
Rg1 1.500E+06 -6.563E-09 -9.844E-05 Rg2 5.000E+05 1.969E-08 9.844E-05 Rd 2.000E+03 -3.063E-15 -6.125E-14 Vdd 1.500E+01 8.750E-04 1.313E-04 Vdrain 0.000E+00 -1.000E-12 0.000E+00
|
Likewise, the results of the sensitivity analysis for the amplifier circuit of Fig. 5.29(b), together with the DC operating point information for the MOSFET, are as follows:
|
**** OPERATING POINT INFORMATION TEMPERATURE = 27.000 DEG C
**** MOSFETS
NAME M1 MODEL nmos ID 2.87E-03 VGS 3.69E+00 VDS 2.96E+00 VBS -6.31E+00 VTH 2.00E+00 VDSAT 1.69E+00
**** DC SENSITIVITY ANALYSIS TEMPERATURE = 27.000 DEG C
DC SENSITIVITIES OF OUTPUT I(Vdrain)
ELEMENT ELEMENT ELEMENT NORMALIZED NAME VALUE SENSITIVITY SENSITIVITY (AMPS/UNIT) (AMPS/PERCENT)
Rg1 1.000E+06 -1.336E-09 -1.336E-05 Rg2 2.000E+06 6.679E-10 1.336E-05 Rd 2.000E+03 -2.867E-15 -5.734E-14 Rs 2.200E+03 -1.149E-06 -2.527E-05 Vdd 1.500E+01 2.672E-04 4.008E-05 Vdrain 0.000E+00 -1.000E-12 0.000E+00
|
Reviewing the above sensitivity results, we see that Spice
has generated several columns of output. The first column indicates the element
that the sensitivity of the drain current ID is taken with respect
to. The second column indicates the nominal value of that element as it appears
in the Spice input file. The third column indicates the sensitivity quantity ![]() where x is
the corresponding element appearing in the leftmost column. The units of this sensitivity
quantity are the units of the output variable specified on the .SENS statement
divided by the units of the element x. For instance, in the case of element RG1,
the sensitivity quantity
where x is
the corresponding element appearing in the leftmost column. The units of this sensitivity
quantity are the units of the output variable specified on the .SENS statement
divided by the units of the element x. For instance, in the case of element RG1,
the sensitivity quantity ![]() is expressed
in A/W. The final column that appears
on the right, is a normalized sensitivity measure. It simply expresses the
sensitivity in more convenient units of A/%. Mathematically, it is written as
is expressed
in A/W. The final column that appears
on the right, is a normalized sensitivity measure. It simply expresses the
sensitivity in more convenient units of A/%. Mathematically, it is written as ![]() where
where ![]() is the
relative accuracy of RG1 expressed in per-cent.
is the
relative accuracy of RG1 expressed in per-cent.
Returning to the results of the two sensitivity analysis, let us consider one interpretation of these results: If we were to build the two amplifiers shown in Fig. 5.29 using resistors that have a tolerance of ±5%, then according to the principle of a total derivative, the total change in the drain current due to variations in the biasing resistors (i.e., RG1, RG2, RD and RS - in the case of the amplifier in Fig. 5.29(b)) can be approximated by the following:
(5.14)

Now, if we assume the worst-case situation, where each resistor undergoes the same amount of change with a sign that contributes to the total sum, as opposed to reduce the sum, then we can write the above equation as,
(5.15)

where we denote the relative magnitude change of each resistor as (DR/R)%. Now, under the assumed worst-case condition, (DR/R)%=5%, we can substitute the sensitivities computed above by Spice into Eqn. (5.15) and determine the expected change in the drain current of the MOSFET in each amplifier of Fig. 5.29. On doing so, we find that for the amplifier with the fixed gate voltage biasing scheme (Fig.5.29(a)) the expected change in the drain current will be about 984.4 uA. Whereas, in the amplifier with a negative feedback biasing scheme (Fig. 5.29(b)), the worst-case change in the drain current is expected to be only 260 uA. This is about 4 times less change than the previous case.
This same type of analysis can be repeated with regards to a variation in the supply voltage VDD. If we consider a 1% change in the supply voltage, then we can expect that the drain current of the MOSFET in the fixed-bias amplifier will experience a 131 uA change. This is contrasted against the amplifier with a negative feedback biasing scheme whose MOSFET drain current will only change by 40 uA.
Unfortunately, the sensitivity analysis seen above does not list the sensitivity relative to the MOSFET. To obtain this information, we use a simple brute-force approach. Consider changing the device parameters K and Vt separately and observe their effect on the drain current through an operating point (.OP) command.
For instance, in the case of the fixed-bias MOSFET amplifier stage shown in Fig. 5.29, consider changing the value of kp=2 mA/V2 on the MOSFET model statement seen in Fig. 5.30 to kp=2.2 mA/V2, a positive change of +10%. Re-running the Spice job, we obtain the following operating point information for the MOSFET:
|
**** MOSFETS
NAME M1 MODEL nmos ID 3.37E-03 VGS 3.75E+00 VDS 8.26E+00 VBS 0.00E+00 VTH 2.00E+00 VDSAT 1.75E+00
|
Thus, the drain current is now 3.37 mA. Comparing this to the drain current prior to the change in kp, listed previously at 3.06 mA, we see that a +10% change in the process transconductance kp results in a +10.1% change in the drain current.
Similarly, if we repeat this same experiment with the MOSFET amplifier having a feedback biasing scheme, that is, consider changing kp of 2 mA/V2 to 2.2 mA/V2 in the Spice deck seen listed in Fig. 5.31 and re-simulating the circuit, we get the following operating point results:
|
**** MOSFETS
NAME M1 MODEL nmos ID 2.90E-03 VGS 3.62E+00 VDS 2.83E+00 VBS -6.38E+00 VTH 2.00E+00 VDSAT 1.62E+00
|
Thus, the drain current becomes 2.90 mA. Comparing this to the drain current prior to the change in kp, listed previously at 2.87 mA, we see that a +10% change in the process transconductance kp results in a +1.04% change in the drain current. This is about 10 times less sensitive to a process change in kp than the fixed biasing scheme.
A similar approach can be taken for changes in the threshold voltage. If we assume that due to a process variation, the threshold voltage of the MOSFET changes by -5%, then we would find for the fixed biasing scheme that the drain current would change by +11.8%. In contrast, the drain current in the MOSFET of the amplifier having a negative feedback biasing scheme would only change by +1.39%.
The benefits of an amplifier biasing scheme that incorporates negative feedback should now be self-evident.
5.6 Integrated-Circuit MOS Amplifiers
In this section we shall investigate the behavior of several different types of fully integratable amplifiers that are constructed with MOSFETs only.
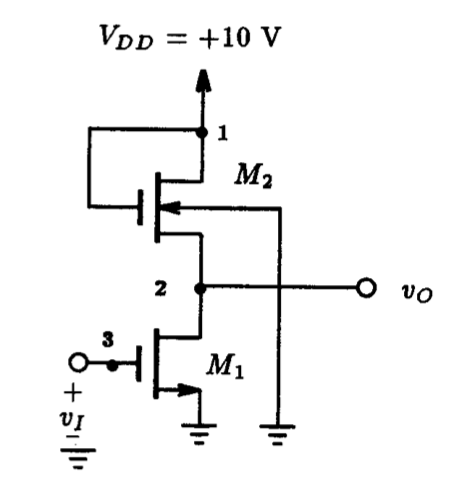
5.5.1 Enhancement-Load Amplifier Including The Body Effect
Fig. 5.32 shows an enhancement-load NMOS amplifier with the substrate connections clearly shown. This arrangement would be typical of an amplifier implemented in an NMOS fabrication process. One important drawback to this amplifier is that its voltage gain is reduced because of the presence of the MOSFET body-effect in transistor M2. To see this, let us consider that the two MOSFETs in the circuit of Fig. 5.32 have the following device parameters: a process transconductance coefficient (unCOX) of 0.25 mA/V2, a zero-bias threshold voltage of 1 V, a channel-length modulation factor lambda of 0.02 V-1, and a body-effect coefficient g of 0.9 V1/2. Transistor M1 will have a length - width dimension of 10 um by 100 um whereas the dimensions of transistor M2 will be reciprocated at 100 um by 10 um. The Spice input file describing this arrangement is listed in Fig. 5.33. A DC sweep of the input voltage level between ground and VDD is requested. For comparison, we shall repeat the same analysis just described on an identical circuit, with identical device parameters except that the body-effect coefficient will be set to zero. The Spice deck for this particular case is simply concatenated on the end of the Spice file shown in Fig. 5.33 and both are submitted to Spice for analysis.
|
Fig. 5.32: An enhancement-load amplifier.
|
An Enhancement-Load Amplifier Including Body Effect
** Circuit Description ** * dc supplies Vdd 1 0 DC +10V * input signal Vi 3 0 DC 0V * amplifier circuit M1 2 3 0 0 nmos L=10u W=100u M2 1 1 2 0 nmos L=100u W=10u * mosfet model statement (by default, level 1) .model nmos nmos (kp=0.25m Vto=+1.0V lambda=0.02 gamma=0.9) ** Analysis Requests ** .OP .DC Vi 0V 10V 100mV ** Output Requests ** .PLOT DC V(2) .Probe .end
Fig. 5.33: The Spice input file for calculating the DC transfer characteristic of the enhancement-load amplifier shown in Fig. 5.32. Each MOSFET is modeled with the effect of transistor body-effect included.
|

Fig. 5.34: The DC transfer characteristic of the enhancement-load amplifier shown in Fig. 5.32 with and without the MOSFET body-effect present.
The results of the analysis are shown in Fig. 5.34. Here the DC transfer characteristics of the enhancement-load amplifier with and without the transistor body-effect present are shown. As is clearly evident, transistor body-effect alters the transfer characteristics of the enhancement-load amplifier significantly. With the input level below one-volt, corresponding to the threshold of M1, the output voltage is held constant at either 9 V or 7.2 V, depending on which characteristic curve one is looking at. In the case of the transfer characteristic curve for the enhancement-load circuit with the body-effect present, with input levels increasing above the one-volt level, the output voltage decreases linearly at a rate of about -7.9 volt-per-volt from its initial 7.2 V level until the input exceeds approximately 1.8 V. At an input of 1.8 V the output is 0.75 V. Above this input voltage level, transistor M1 leaves the saturation-region and enters the triode region, resulting in the amplifier characteristics becoming nonlinear.
In the case of the amplifier with the body-effect eliminated, with inputs above 1 V, the output level (beginning at 9 V) decreases linearly at a rate of -9.2 volt-per-volt. Like the previous case, when the input voltage level exceeds 1.8 V (and the output at 0.75 V), transistor M1 enters the triode region and the amplifier characteristic curve becomes nonlinear. Comparing these details to that of the enhancement-load amplifier with the body-effect included suggest that the presence of transistor body-effect has decreased the effective gain of this enhancement-load amplifier.
To further demonstrate this, let us compute the voltage gain of this amplifier, with and without the body-effect present, using the transfer function (.TF) analysis command of Spice with the amplifier biased in its linear region. For illustrative purposes, we shall bias the input to the amplifier at 1.5 V since this input level maintains both amplifiers in their linear region. Modifying each of the two Spice decks used previously, by changing the source statement to read as follows
Vi 3 0 DC +1.5V
and including the following .TF command
.TF V(2) Vi.
The results of the two small-signal transfer function analyses are then found in their respective output files. In the case of the enhancement-load amplifier with body-effect present, the results are:
|
**** SMALL-SIGNAL CHARACTERISTICS
V(2)/Vi = -7.316E+00
INPUT RESISTANCE AT Vi = 1.000E+20
OUTPUT RESISTANCE AT V(2) = 5.508E+03 |
For the case of the enhancement-load amplifier with the body-effect eliminated, the results are:
|
**** SMALL-SIGNAL CHARACTERISTICS
V(2)/Vi = -9.027E+00
INPUT RESISTANCE AT Vi = 1.000E+20
OUTPUT RESISTANCE AT V(2) = 6.677E+03 |
The above two sets of results, therefore, re-confirm our earlier claim that the MOSFET body-effect acts to decrease the effective-gain of an enhancement-load amplifier.
Before we leave this section, it would be instructive to confirm that the small-signal formula for the voltage gain of this amplifier including transistor body-effect is accurate. According to the development provided in Section 5.9 of Sedra and Smith, 3rd Edition, the voltage gain of the amplifier shown in Fig. 5.32 is given by the following equation: write the above equation as,
(5.16)

Through an operating point (.OP) analysis command (included in the previous analysis), we found the following values for the small-signal model parameters of each transistor:
|
**** MOSFETS
NAME M1 M2 MODEL nmos nmos ID 3.32E-04 3.32E-04 VGS 1.50E+00 6.87E+00 VDS 3.13E+00 6.87E+00 VBS 0.00E+00 -3.13E+00 VTH 1.00E+00 2.04E+00 VDSAT 5.00E-01 4.83E+00 GM 1.33E-03 1.37E-04 GDS 6.25E-06 5.84E-06 GMB 7.72E-04 3.20E-05 |
Substituting the appropriate values into Eqn. (5.16), we find AV=-7.344 V/V. This is very close to the value predicted directly by Spice above (i.e., AV=-7.316 V/V). If the output conductance’s are neglected in this calculation, then we would find AV=-7.869 V/V. This result, for most practical applications, would be more than adequate.
|
Fig. 5.35: A CMOS amplifier with current source biasing.
|
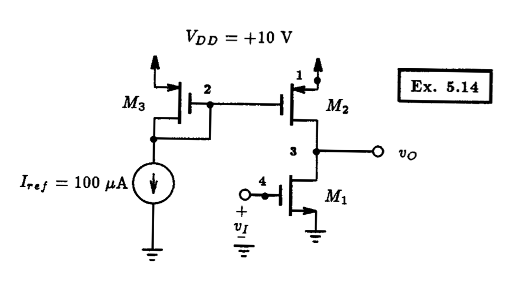
Example 5.14: A CMOS Amplifier
** Circuit Description ** * dc supplies Vdd 1 0 DC +10V Iref 2 0 DC 100uA * input signal Vi 4 0 DC 0V * amplifier circuit M1 3 4 0 0 nmos L=10u W=100u M2 3 2 1 1 pmos L=10u W=100u M3 2 2 1 1 pmos L=10u W=100u * mosfet model statements (by default, level 1) .model nmos nmos (kp=20u Vto=+1V lambda=0.01) .model pmos pmos (kp=10u Vto=-1V lambda=0.01) ** Analysis Requests ** * calculate DC transfer characteristics .DC Vi 0V +10V 10mV ** Output Requests ** .PLOT DC V(3) .probe .end
Fig. 5.36: The Spice input file for calculating the DC transfer characteristic of the CMOS amplifier circuit shown in Fig. 5.35. |
5.5.2 CMOS Amplifier
As an example of an amplifier that is fully integratable using MOS technology, we display in Fig. 5.35 a CMOS amplifier with an active current-source load. Using Spice, we would like to compute and plot the amplifier DC transfer characteristic (i.e., vO vs. vI). This particular circuit was presented in Example 5.14 of Sedra and Smith, 3rd Edtion, where it was assumed that Vtn=|Vtp|=1 V, unCOX=2upCOX=20 uA/V2}, and lambda=0.01 V-1 for n and p devices. Furthermore, for all devices it was assumed that W=100 um and L=10 m.
The Spice input file corresponding to this CMOS amplifier is listed in Fig. 5.36. A zero-valued DC voltage source VI is initially applied to the input of the amplifier and will be varied over a range of values beginning at ground potential and increasing to VDD in small 10 mV steps. The output voltage (V(3)) will then be plotted as a function of the input voltage VI.
The DC transfer characteristic of the CMOS amplifier, as calculated by Spice, is shown in Fig. 5.37. Here we see that the output voltage is very nearly 10 V for input signals less than about +1.0 V and near ground potential when the input level exceeds +2.5 V. Between these two values, the output voltage begins to change value in a somewhat gradual fashion, except around the 2 V input level. Here the output level changes quite dramatically, albeit in a linear manner. Thus, the CMOS amplifier experiences large voltage gain in the vicinity of the 2 V input level.
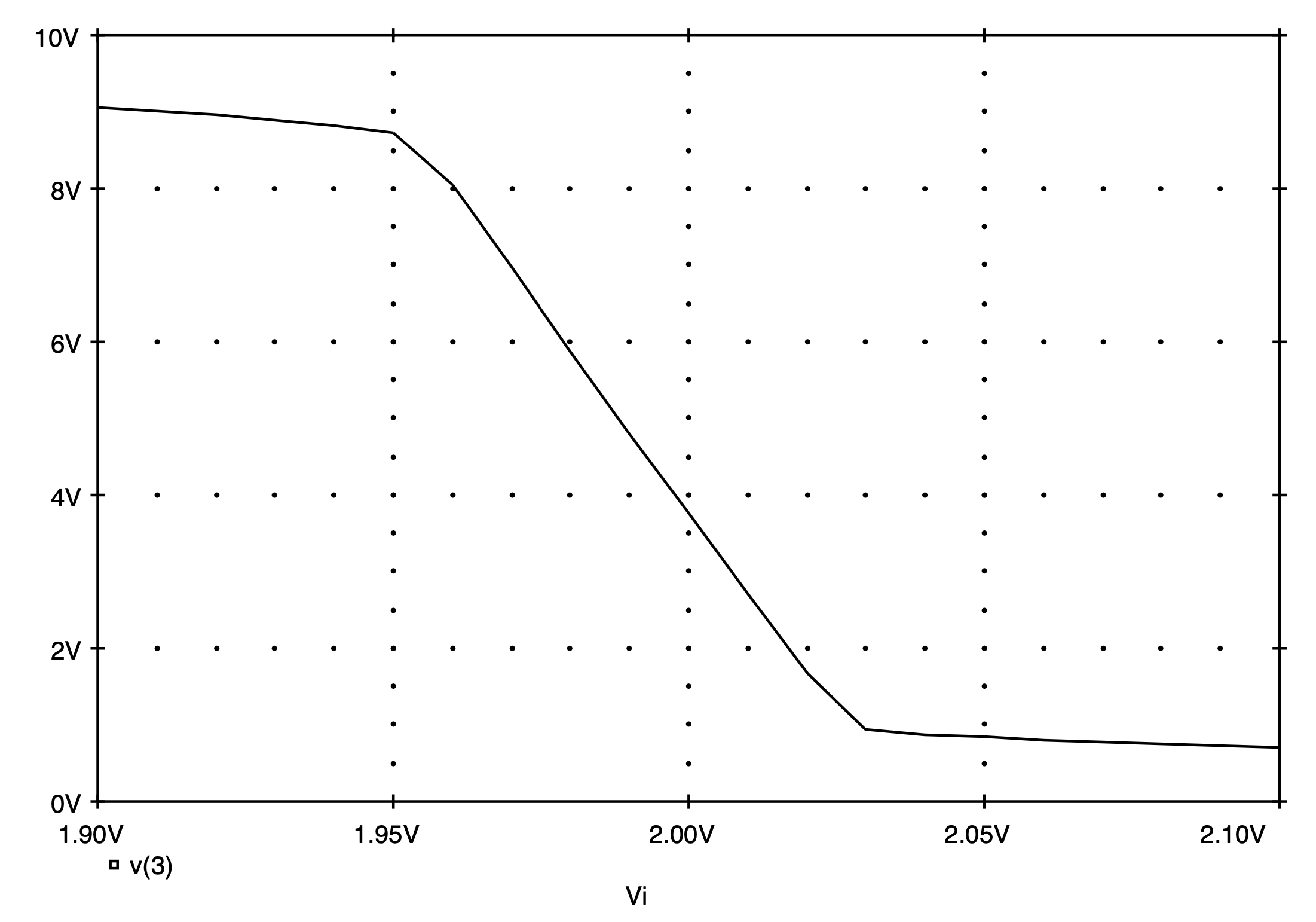
To see the high-gain region of this amplifier more closely, we will repeat the previous DC sweep analysis and evaluate the amplifier transfer characteristic ranging between +1.9 V and +2.1 V. A very small step-size of 100 uV is used to obtain a smooth curve through the high-gain region of the amplifier. The results are shown in Fig. 5.38. The linear region of the amplifier is clearly visible. It is bounded between input voltages of 1.955 V and 2.027 V. Correspondingly, the output voltage varies between 8.589 V and 0.9966 V. This suggests that the gain of this amplifier in this linear region is approximately (8.589 - 0.9966)/(1.955 - 2.027) = - 118.9 V/V.
A similar result is also obtained when the small-signal gain is evaluated around a single operating point inside this linear region. Consider this point to be midway between the extremes of the linear region; this would correspond to an input bias level of about 2 V. Modifying the Spice input deck shown in Fig. 5.36 so that the input is biased at 2 V and replacing the DC sweep command seen there by a .TF analysis command, one would find in the Spice output file the following small-signal DC transfer function information:
|
**** SMALL-SIGNAL CHARACTERISTICS
V(3)/Vi = -1.050E+02
INPUT RESISTANCE AT Vi = 1.000E+20
OUTPUT RESISTANCE AT V(3) = 5.059E+05
|
Thus, the small-signal gain of the CMOS amplifier is -105 V/V at an input DC voltage level of 2 V.
It is interesting to note that the simple formula for the voltage gain in the linear region of the CMOS amplifier shown in Fig. 5.35 derived in Section 5.9 of Sedra and Smith, 3rd Edition, and repeated here below,
(5.17)

results in a gain value that is quite close to that computed by Spice above. Substituting the appropriate device parameter values into Eqn. (5.17), we get AV=-100 V/V.
|
Fig. 5.37: The DC transfer characteristic of the CMOS amplifier shown in Fig. 5.35 as calculated by Spice.
|
Fig. 5.38: An expanded view of the large-signal transfer characteristic of the CMOS amplifier shown in Fig. 5.35 in its high-gain region.
|
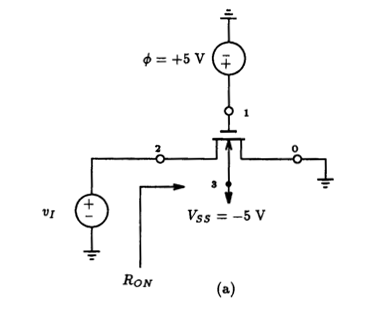
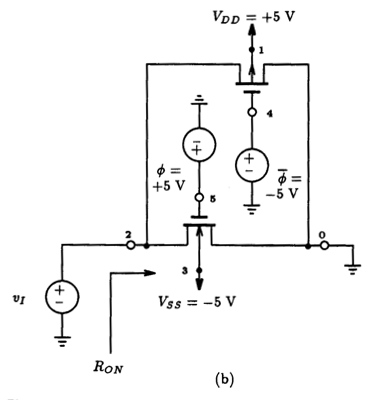
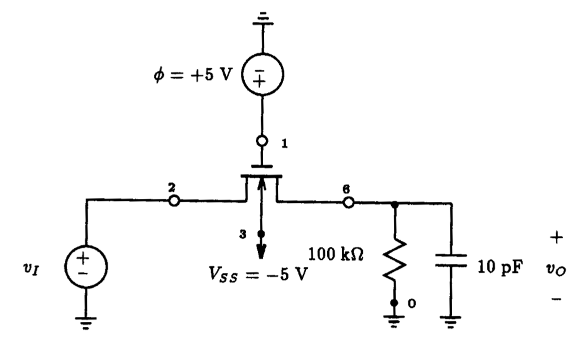
5.6 MOSFET Switches
MOSFETs are commonly used as switches for both analog and digital signals. In analog circuit applications, a switch is used to control the passage of an analog current signal between two nodes in a circuit, in either direction, without distortion or attenuation. In digital applications, a switch is commonly used as a transmission gate to realize specific logic functions when combined with other logic gates.
Fig. 5.39: (a) An ideal mechanical switch (b) Electrical equivalent of a real switch with on-resistance RON.
An ideal mechanical switch is depicted in Fig. 5.39(a). In the ``on’’ state, i.e., switch closed, a direct connection is made between nodes 1 and 2. Thus, a signal applied to node 1 will also appear at node 2. The reverse is also true if nodes 1 and 2 are interchanged. In practise, a signal passing through a switch will experience a signal attenuation due to the electrical resistance of the switch. Thus, we can model this behavior by adding a resistance RON in series with the ideal switch, as illustrated in Fig. 5.39(b). Clearly then, the larger RON, the more loss a signal will experience as it passes through the switch.
To judge the on-resistance of a single n-channel MOSFET switch, let us create a Spice input file that represents the situation shown in Fig. 5.40(a). In this circuit, we shall sweep the input voltage vI from VSS=-5 V to VDD=+5 V and compute the current that is supplied to the switch by vI. The other terminal of the MOSFET switch is connected directly to ground, thus the resistance of the switch RON is given by the ratio of the input voltage to the current supplied by this voltage source. The gate of the MOSFET, being the control terminal of the switch, will be held at VDD=+5 V to ensure that the switch is turned-on. The resulting Spice input file is shown in Fig. 5.41. The NMOS transistor will be assumed to have a process transconductance parameter unCOX equal to 0.25 mA/V2, a zero-bias threshold voltage of 1 V, a channel-length modulation factor lambda of 0.02 V-1, and a body-effect coefficient g of 0.9 V1/2. The dimensions of the MOSFET will be 100 um by 100 um.
It should be pointed out that the DC sweep was selected to have a voltage step of 10.01 mV instead of a more even 10 mV. This is to ensure that when we compute the ratio of input voltage to input current, we don't try and divide 0 by 0. Moreover, our choice of which terminal of the MOSFET is the source, and which is the drain, was arbitrary. The results should be same regardless of our choice. (If there is any doubt, the reader should repeat the simulation with the source and drain terminals interchanged).
On completion of Spice, we divide the input voltage by the input current and plot the results as a function of the input voltage. The curve representing this result is shown in Fig. 5.42 and is labeled as the NMOS switch. As is evident, the on-resistance of the switch is lowest at RON=560 W when the input equals VSS=-5 V. The switch on-resistance steadily increases as the input voltage increases towards VDD=+5 V. In fact, as the input voltage approaches VDD, the switch on-resistance increases substantially, e.g., at vI=+5 V, RON=5.6 kW. We can conclude that the on-resistance of this switch is dependent on the input signal level, which introduces undesirable nonlinearity.
|
|
Computing Switch On-Resistance Of A NMOS Switch
** Circuit Description ** * Input signal Vi 2 0 DC 0V * Substrate Bias Vss 3 0 DC -5V * Control Signal Vphi 1 0 DC +5V * Switch: NMOS Transistor M1 2 1 0 3 nmos_enhancement_mosfet L=100u W=100u * mosfet model statement (by default, level 1) .model nmos_enhancement_mosfet nmos (kp=0.25m Vto=+1.0V lambda=0.02 gamma=0.9) ** Analysis Requests ** * sweep the input voltage from Vss to Vdd (skip over 0,0 point) .DC Vi -5V +5V 10.01mV ** Output Requests ** .PLOT DC I(Vi) V(2) .Probe .end
Fig. 5.41: The Spice input file for calculating the input current as a function of input voltage for the n-channel MOSFET switch of Fig. 5.39(a). Post-processing will be used to compute the on-resistance of the switch.
|
|
Fig. 5.40: MOSFET switch realizations: (a) a single n-channel MOSFET (b) a CMOS transmission gate.
|
Computing Switch On-Resistance Of A CMOS Switch
** Circuit Description ** * Input signal Vi 2 0 DC 0V * Substrate Bias Vdd 1 0 DC +5V Vss 3 0 DC -5V * Control Signal Vphi 4 0 DC -5V Vphibar 5 0 DC +5V * Switch: NMOS + PMOS Transistors M1 2 5 0 3 nmos_enhancement_mosfet L=100u W=100u M2 2 4 0 1 pmos_enhancement_mosfet L=100u W=100u * mosfet model statement (by default, level 1) .model nmos_enhancement_mosfet nmos (kp=0.25m Vto=+1.0V lambda=0.02 gamma=0.9) .model pmos_enhancement_mosfet pmos (kp=0.25m Vto=-1.0V lambda=0.02 gamma=0.9) ** Analysis Requests ** * sweep the input voltage from Vss to Vdd (skip over 0,0 point) .DC Vi -5V +5V 10.01mV ** Output Requests ** .PLOT DC I(Vi) V(2) .Probe .end
Fig. 5.42: The on-resistance RON as a function of the input signal level of an analog switch realized as: (a) a single n-channel MOSFET, or (b) a single p-channel MOSFET, (c) a parallel combination of an n-channel and p-channel MOSFETs.
|

Fig. 5.43: The Spice input file for calculating the input current as a function of input voltage for the CMOS transmission gate of Fig. 5.39(b). Post-processing will be used to compute the on-resistance of the switch.
If we repeat the above experiment on a p-channel MOSFET, similar results would result. These are also shown in Fig. 5.42. Clearly, the PMOS switch has similar behavior, but in a complementary manner. Observing these results, we can conclude that a single MOSFET does not make for a very effective switch.
A better approach, and one that is extensively used in analog IC design when a high-quality switch is required, is to connect both the n-channel and the p-channel MOSFETs in parallel as illustrated in Fig. 5.40(b). The gate control of each MOSFET is driven by complementary signals. To see why this transistor arrangement makes for an effective switch, let us compute the on-resistance of this switch. To turn on the switch, control signal f is set to VDD=+5 V and f-bar is set to VSS=-5 V. The Spice input file describing the situation is listed in Fig. 5.43. The MOSFETs are assumed to have the same device parameters used in the previous example. For easy comparisons, the Spice results for this CMOS switch are shown superimposed on the same graph of on-resistance of the NMOS and PMOS switches. Clearly, the on-resistance of the CMOS transmission gate is much more constant than was the case for a single MOSFET switch. Furthermore, the on-resistance of the CMOS switch is much lower than that of the previous two switches. The on-resistance is seen to vary between 500 W and 800 W, with the maximum on-resistance occurring when the input signal is zero.
This example did not show another limitation of the single transistor switch, namely, its limited range of operation which is caused by its non-zero threshold voltage. To illustrate this limitation, consider the switch arrangement shown in Fig. 5.44. Here a single n-channel MOSFET is connected between the voltage source vI and a load consisting of a 100 kW resistor and a 10-pF capacitor. The n-channel MOSFET is assumed identical to that just described above. Moreover, the gate of this MOSFET is biased at +5 V, intended to turn the switch fully on. The Spice deck for this case is provided in Fig. 5.45. Now if we simulate the action of this switch using Spice with a 10 V step input beginning at -5 V, then, instead of the voltage at the output following the input in its entirety, we see that the output voltage actually clamps at a level of about 1.85 V as seen in Fig. 5.46. It is easily shown that this clamping limit depends on the threshold voltage of the MOSFET (see Sedra and Smith), but it may not be quite so obvious that this clamping limit also depends on the i-v characteristics of the switch. To convince oneself of this, consider increasing the size of the transistor so that its i-v characteristics change. For example, let us increase the width of the MOSFET to 500 um. On re-running the Spice simulation, we find that the output voltage has similar behavior as in the previous case except that the output voltage clamps at a higher voltage of 2.0 V. This is also shown in Fig. 5.46. The reason for this behavior is because the MOSFET must supply a continuous current to the RC load in order to sustain the output voltage.
|
Fig. 5.44: Circuit arrangement illustrating the effect of MOSFET threshold voltage on the switch range of operation.
|
The Effect Of The Threshold Voltage On Switch Operation
** Circuit Description ** * Input signal Vi 2 0 DC 0V PWL (0 -5V 100ns -5V 200ns 5V 10ms 5V) * Substrate Bias Vss 3 0 DC -5V * Control Signal Vphi 1 0 DC +5V * Switch: NMOS Transistor M1 2 1 6 3 nmos_enhancement_mosfet L=100u W=100u * Load resistor Rload 6 0 100k Cload 6 0 10pF * mosfet model statement (by default, level 1) .model nmos_enhancement_mosfet nmos (kp=0.25m Vto=+1.0V lambda=0.02 gamma=0.9) ** Analysis Requests ** .TRAN 1ns 500ns 0ns 1ns ** Output Requests ** .PLOT TRAN V(6) .Probe .end
Fig. 5.45: The Spice input file for calculating the step response of the NMOS switch arrangement shown in Fig. 5.44. |
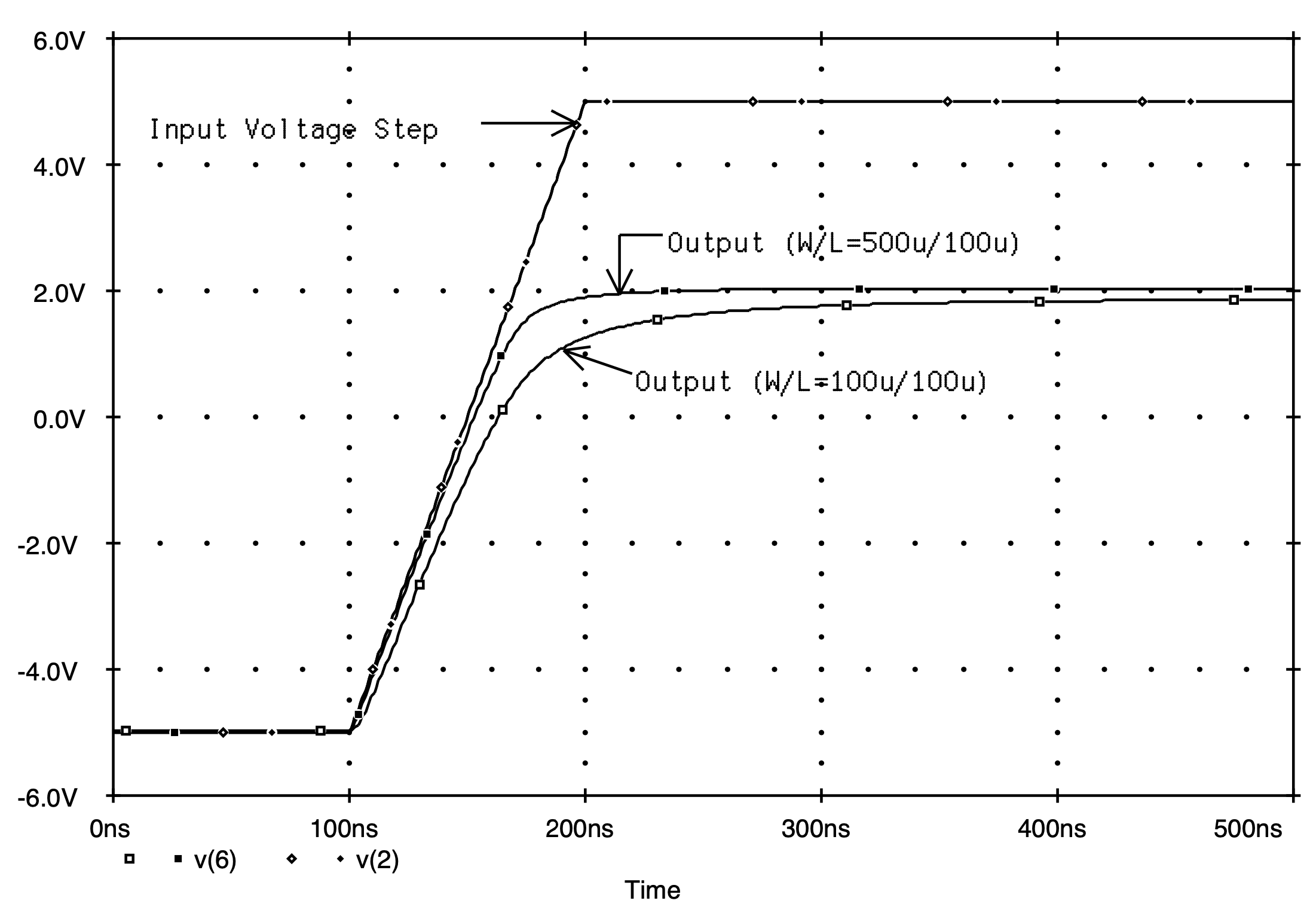
Fig. 5.46: The step response of a NMOS switch arrangement shown in Fig. 5.44 for two different sized MOSFETs.
5.7 Describing MESFETs To PSpice
Built-in models for metal-semiconductor FETs (MESFETs) do not exist in Spice (versions 2G6 and earlier). Instead, we shall rely on the built-in MESFET model of PSpice to carry out our simulation of circuits containing MESFETs.
MESFETs are described to PSpice in the exact same way as any other semiconductor device is described to Spice; that is, using an element statement and a model statement. The following outlines the syntax of these two statements, including the details of the built-in MESFET model of PSpice.
|
Fig. 5.47: PSpice element description for the n-channel depletion-mode GaAs MESFET. Also listed is the general form of the associated MESFET model statement. A partial listing of the parameters applicable to the n-channel MESFET is given in Table 5.5.
|
Fig. 5.48: The PSpice large-signal MESFET model under static conditions.
|

Table. 5.5: A partial listing of the PSpice parameters for the LEVEL 1 MESFET model.
5.7.1 MESFET Element Description
MESFETs are described in a PSpice listing using an element statement beginning with a unique name prefixed with the letter B. This is followed by a list of nodes that the drain, gate, and source of the MESFET are connected to. Subsequently, in the next field, a name of a model characterizing the particular MESFET is given - more on this in a moment. The final field of this statement is optional, and its purpose is to allow one to scale the size of the device by declaring the number of MESFETs connected in parallel. A summary of the element statement syntax for the n-channel MESFET is provided in Fig. 5.47. Included in this list is the corresponding syntax for the MESFET model statement (.MODEL) that must be present whenever a MESFET is made reference to. This statement defines the terminal characteristics of the MESFET by specifying the values of particular parameters in the MESFET model. Parameters not specified in the model statement are assigned default values by PSpice. Details of this model will be discussed briefly next.
5.7.2 MESFET Model Description
As is evident from Fig. 5.47, the model statement for the n-channel MESFET begins with the keyword .MODEL and is followed by the name of the model used by a MESFET element statement, the nature of the MESFET (i.e., GASFET), and a list of the parameters characterizing the terminal behavior of the MESFET is enclosed between brackets. The parameters describing the terminal characteristics of the MESFET are quite similar to those used to describe the JFET above. An additional parameter (a) has been added to properly account for the early saturation phenomenon of the MESFET [Hodges and Jackson, 1983].
The general form of the DC Spice model for an n-channel MESFET is illustrated schematically in Fig. 5.48. The bulk resistance of the drain, gate, and source regions of the MESFET are lumped into three linear resistances rD, rG, and rS, respectively. The DC characteristic of the intrinsic MESFET is determined by the nonlinear dependent current source iD and the two Schottky-barrier diodes. These two Schottky diodes represent the metal semiconductor junctions that define the channel region. The functional description of the drain current iD can take on three different forms depending on the value assigned to the parameter LEVEL that appears on the MESFET model statement. PSpice defaults to a LEVEL 1 model when none is specified. The LEVEL 1 MESFET model is probably the most widely used of the three and will be the only one discussed here. Details pertaining to the other models can be found in the PSpice Users' Manual.
The equation describing the drain current for the LEVEL 1 MESFET model is given below:
(5.18)

Here the same equation is used to describe both the triode and saturation regions of the device; the distinction between the two is provided by the factor tanh(avDS). This factor does also account for the early saturation phenomenon observed in MESFETs. See the i-v characteristics in Fig. 5.49 for a typical MESFET having device parameters Vt=-1 V, b=10-4 A/V2, W=100 um, L=1 um, lambda=0.05 V-1, and a taking on values of 0.5, 1.0, and 2.0. As an extreme limit, the i-v characteristic for a=10^6 is also included. In these equations, b and lambda have the same meaning as in the Spice JFET model. That is, b is the device transconductance parameter, and lambda is the channel-length modulation coefficient.
A partial listing of the parameters associated with the Spice MESFET model under static conditions is given in Table 5.5. Also listed are the associated default values which a parameter assumes if a value is not specified for it on the .MODEL statement. To specify a parameter value one simply writes, for example: level=1, beta=20u, Vto=-1V, etc.
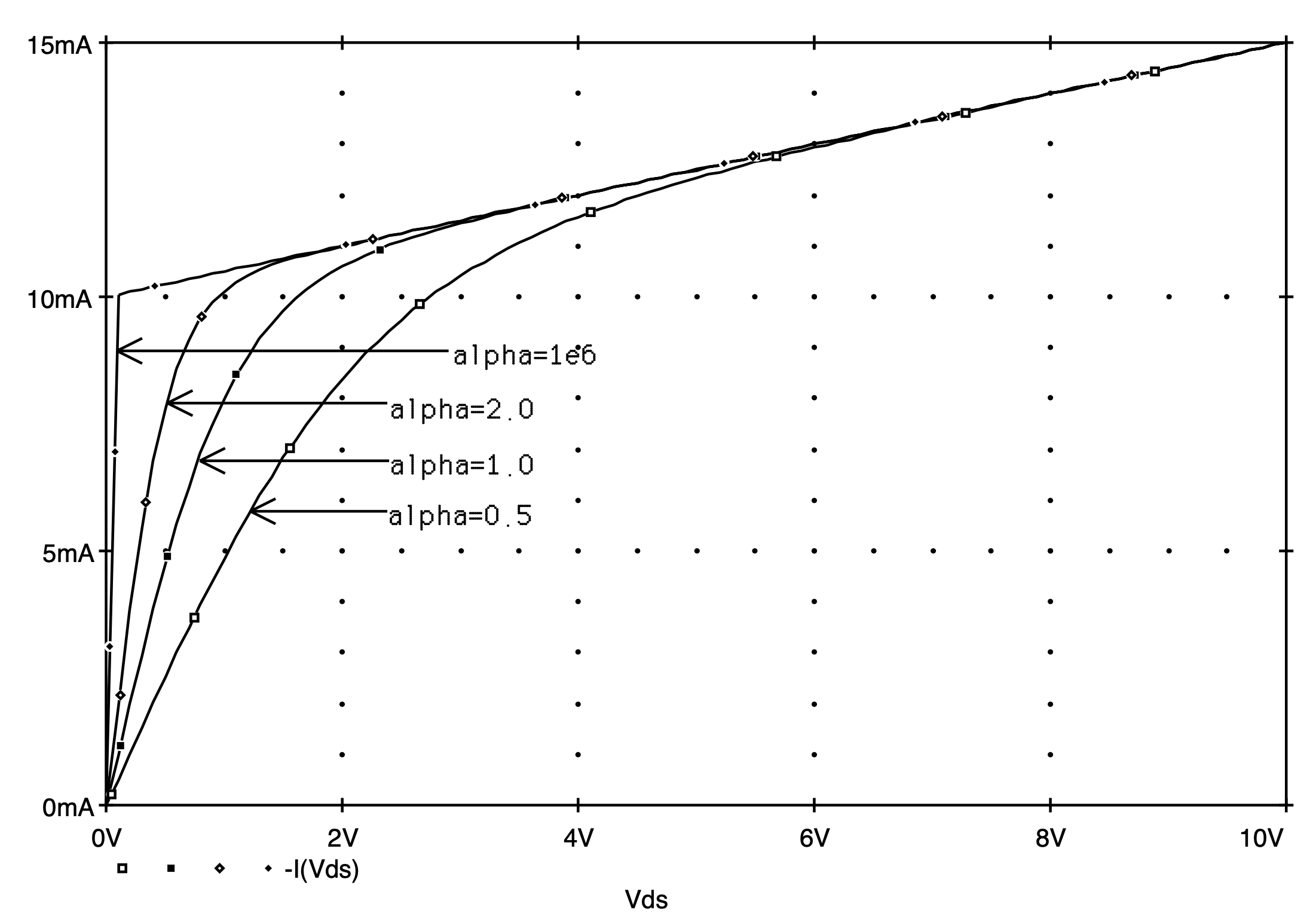
Fig. 5.49: Illustrating the dependence of the i-v characteristic of a single MESFET on the value of a.
5.7.3 Small-Signal MESFET Model
The linear small-signal model of the n-channel MESFET is identical to that seen previously for the JFET in Fig. 5.26(b). It consists of a single voltage-controlled current source having transconductance gm. Here gm is the MESFET transconductance and is related to the DC bias according to the following:
(5.18)
![]()
Likewise, the output conductance gds, which is also equal to 1/ro, is computed according to the following:
(5.20)
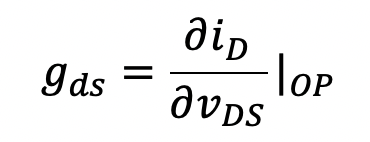
|
Fig. 5.50: A MESFET amplifier with MESFET load.
|
Example 5.15: A MESFET Amplifier
** Circuit Description ** * dc supplies Vdd 1 0 DC +10V * input signal Vi 3 0 DC -0.3V * amplifier circuit B1 2 3 0 n_mesfet 100 B2 1 2 2 n_mesfet 50 * mesfet model statements (by default, level 1) .model n_mesfet gasfet (beta=0.1m Vto=-1.0V lambda=0.1) ** Analysis Requests ** * calculate DC transfer characteristics .DC Vi -10V +1V 0.01V ** Output Requests ** .PLOT DC V(2) .probe .end
Fig. 5.51: The Spice input file for calculating the DC transfer characteristic of the MESFET amplifier circuit shown in Fig. 5.50.
|
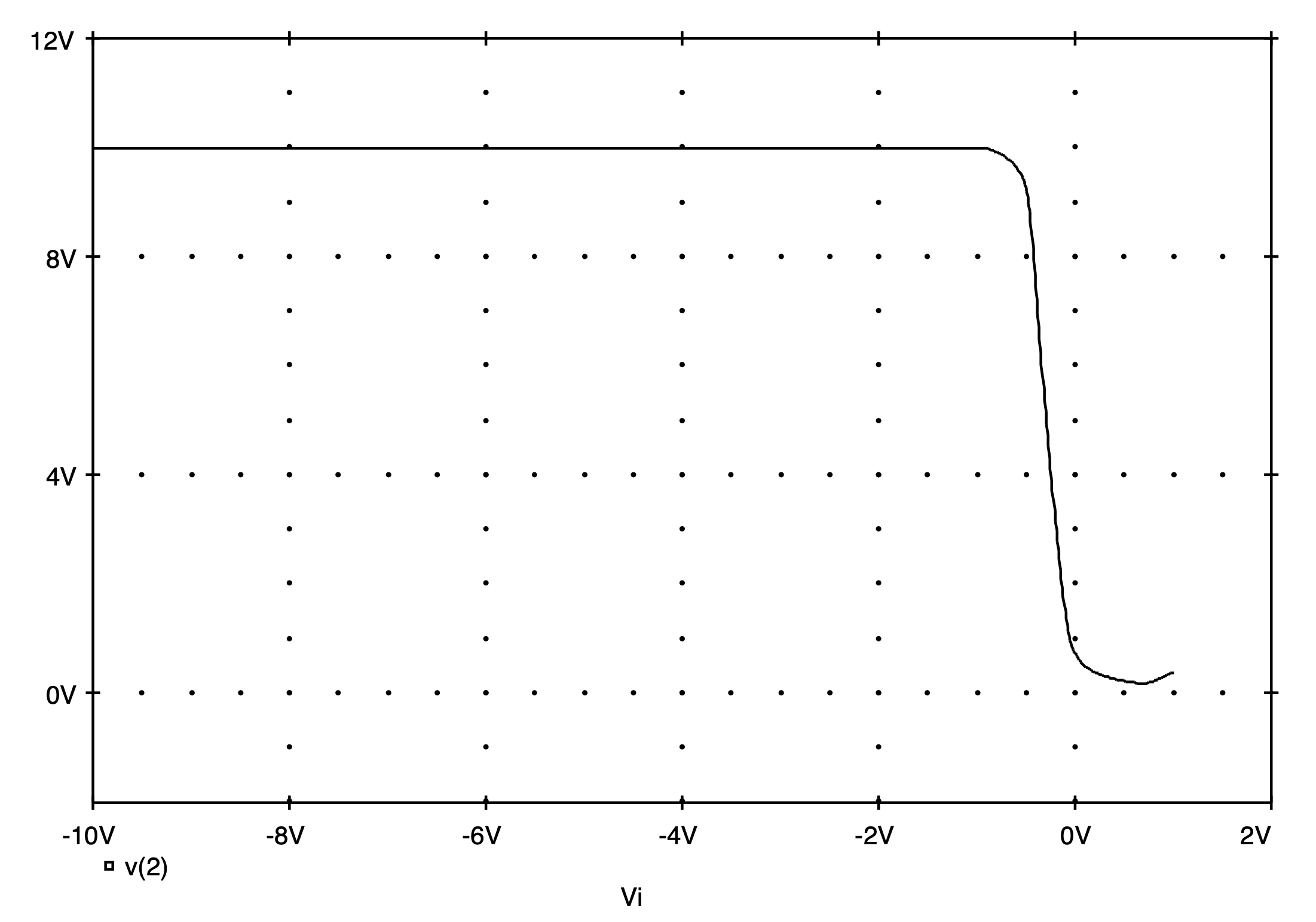
Fig. 5.52: The DC transfer characteristics of the MESFET amplifier shown in Fig. 5.50 as calculated by PSpice.
5.7.4 A MESFET Biasing Example
As an example of an application of GaAs MESFETs, in Fig. 5.50 we display a simple MESFET amplifier circuit. The lengths of the two devices are assumed to be equal to the minimum value for a particular technology (1 um in this case). Whereas, the width dimensions of B1 and B2 are W1=100 um and W2=50 um, respectively. The characteristics of the GaAs process is specified in terms of the electrical parameters of minimum sized devices (i.e., L=1 um and W=1 um), and will be assumed to be: Vt=-1 V, b=10-4 A/V2} and lambda=0.1 V-1. To determine the parameters of a particular device, it is a simple matter to scale the appropriate parameters of the unit-sized device. Alternatively, we can let PSpice perform this scaling operation for us. We shall illustrate the latter, since PSpice is less likely to make a mistake than we are.
Using the device parameters for the minimum-sized device, we can establish the following PSpice model statement for the unit-sized n-channel MESFET:
.model n_mesfet gasfet (beta=0.1m Vto=-1.0V lambda=0.1)
Parameters not specified will, as usual, assume default values.
To account for the different widths of the two transistors, we simply specify on the element statement of each MESFET the ratio of the transistor width to the unit-sized width. In this case, the unit-sized width is 1 um, so for B1 with a device width of 100 um one would specify a scale factor of 100. Of course, this has identical meaning as connecting 100 unit-sized transistors in parallel. Likewise, one would specify a scale factor of 50 for the other transistor. To illustrate, consider the element statement for transistor B1 is
B1 2 3 0 n_mesfet 100.
With the aid of Spice, we would like to determine the DC transfer characteristics of this amplifier. This is easily performed using the PSpice listing given in Fig. 5.51. Here we are sweeping the input voltage level between -10 V and +1 V in 10 mV steps. The input voltage should normally remain negative, otherwise the input metal-semiconductor junction of B1 (the gate-source Schottky diode) becomes forward biased. For demonstration purposes, we are allowing the input voltage to go slightly positive in order to observe the effect of forward biasing this junction.
The resulting DC transfer characteristics of this MESFET amplifier are on display in Fig. 5.52. Here we see that the amplifier has inverter-like characteristics, with its high gain region in the vicinity of a -0.3 V input level. When the input signal level goes more positive than 0.7 V we see that the output voltage begins to rise, corresponding to the fact the input metal-semiconductor junction of the MESFET has become forward biased and that the gate voltage no longer controls the drain-to-source current. Using the transfer function (.TF) command we can determine the voltage gain in the high-gain region of the amplifier. This requires that we bias the input to the amplifier at -0.3 V, as is already shown in the Spice deck of Fig. 5.51. Further, we need to change the analysis request from a DC sweep to the following small-signal transfer function command:
.TF V(2) Vi
We also include an operating point command (.OP) to obtain the small-signal model parameters.
On completion of Spice, we find the following small-signal characteristics associated with the MESFET amplifier:
|
**** SMALL - SIGNAL CHARACTERISTICS
V(2) / Vi = -2.143E+01
INPUT RESISTANCE AT Vi = 4.269E+10
OUTPUT RESISTANCE AT V(2) = 1.010E+03
|
Here we see that the gain in the linear region of the MESFET amplifier is -21.43 V/V, about a factor of 5 times less than the gain available with the simple CMOS amplifier discussed previously in Section 5.6. This result seems to correspond directly with the result that the output resistance for the MESFET amplifier is about five times lower than the output resistance of the CMOS amplifier.
The small-signal model parameters of the two MESFETs as calculated by PSpice are found in the output file as follows:
|
**** GASFETS
NAME B1 B2 MODEL n_mesfet n_mesfet ID 7.42E-03 7.42E-03 VGS -3.00E-01 0.00E+00 VDS 5.15E+00 4.85E+00 GM 2.12E-02 1.48E-02 GDS 4.90E-04 5.00E-04
|
It is re-assuring that when these values are substituted into the formula for the small-signal voltage gain given by AV = - gm (ro1||ro2) we get very similar results to those computed above using the .TF command (i.e., AV=-21.41 V/V).
5.9 Spice Tips
· FETS are described to Spice using an element statement and a model statement. The element statement describes the connections that the FET makes to the rest of the network and the name of the model that specifies its terminal behavior. The model statement assigns particular values to internal parameters of the built-in FET model of Spice. Parameters whose values are not specified on the model statement are assigned default values.
· Spice has built-in models for MOSFETs and JFETs.
· PSpice has built-in models for MOSFETs and JFETs, and in addition MESFETs.
· Vt0 is positive for enhancement-mode n-channel MOSFETs and depletion-mode p-channel MOSFETs.
· Vt0 is negative for depletion-mode n-channel MOSFETs and enhancement-mode p-channel MOSFETs.
· Vt is negative for both n-channel and p-channel JFETs.
· Vt is negative for an n-channel depletion MESFET and is positive for the n-channel enhancement MESFET.
· The sensitivity analysis command of Spice (.SENS) does not compute the sensitivities of the circuit variables to the parameters of the MOSFET model. These must be computed directly by perturbing each parameter of the MOSFET model and observing its effect.
· A small-signal analysis of an amplifier should always be computed around a known operating point and one that is normally within the linear region of the amplifier. The best way to determine the appropriate operating point is by first performing a DC sweep of the input voltage over the range defined by the power supplies and locating the linear region of the amplifier. The input to the amplifier is then biased inside this region where Spice can compute the small-signal behavior.
5.10 Bibliography
A. Vladimirescu and S. Liu, The simulation of MOS integrated circuits using SPICE2, Memorandum no. M80/7, February 1980, Electronics Research Laboratory, University of California, Berkeley.
R.L. Geiger, P. E. Allen and N. R. Strader, VLSI Design Techniques For Analog And Digital Circuits, New York: McGraw-Hill, 1990.
Staff, PSpice Users' Manual, MicroSim Corporation, Irvine, California, Jan. 1991.
D.A. Hodges and H. Jackson, Analysis and Design of Digital Integrated Circuits, New York: McGraw-Hill, 1983.
5.11 Problems
5.1. Let an n-channel enhancement transistor for which uCOX=50 uA/V2, W=L=25 um and Vt=2 V be operated with VGS=6 V. Find iD for vDS=2 V using Spice. Repeat with vDS=6 V.
5.2. An enhancement PMOS transistor has uCOX=40 uA/V2, L=25 m, W=50 m, Vt=-1.5 V, and lambda = 0.02 V-1. The gate is connected to ground and the source to +5 V. Find the drain current using Spice for (a) vD=4 V, (b) vD=+1.5 V, (c) vD=0 V, and (d) vD=-5 V.
5.3. A depletion-type n-channel MOSFET with uCOX=4 mA/V2 and Vt=-3 V has its source and gate grounded. With the aid of Spice, find the region of operation and the drain current for (a) vD=0.1 V, (b) vD=1 V, (c) vD=3 V, and (d) vD=5 V. How do these results compare with hand analysis? Repeat with lambda = 0.05 V-1.
5.4. A depletion-type PMOS transistor has IDSS=8.8 mA, Vt=+2.2 V and lambda = 0.04 V-1. The source is connected to ground, the gate is connected to -2 V and a 2-mA current is pulled from the drain, using Spice determine the source-drain voltage. Assume that the width of the MOSFET is twice that of its length. Compare your results with a hand analysis.
5.5. Design the circuit of Fig. 5.3 to establish a drain current of 1 mA and a drain voltage of 0 V. The MOSFET has Vt=2 V, uCOX=20 A/V2, L= 10 m and W=400 m. Confirm your design using Spice. How much does the drain current change (in percent) when the effect of channel-length modulation is included in the Spice model of the MOSFET (assume lambda = 0.04 V-1)?
5.6. Using Spice as a curve tracer, plot the iD - vDS characteristics of an enhancement-mode n-channel MOSFET having uCOX=50 uA/V2, L=25 um, W=50 um, Vt=+1.5 V, and lambda =0.04 V-1. Provide curves for VGS=1, 2, 3, 4 and 5 volts. Show the characteristics for vDS up to 10 V.
5.7. Using Spice as a curve tracer, plot the iD - vDS characteristics of a depletion-mode p-channel MOSFET having uCOX=50 uA/V2, L=25 um, W=50 um, Vt=+1.2 V, and lambda = 0.04 V-1. Provide curves for VGS=-1, -2, -3, -4 and -5 volts. Show the characteristics for vDS from 0 to -10 V.
5.8. Consider an n-channel JFET with IDSS=4 mA and VP=-2 V. If the source is grounded and a -1 V dc voltage source is applied to the gate, using Spice find the drain current that corresponds to the minimum drain voltage that results in pinch-off operation.
5.9. For a JFET having VP=-2 V and IDSS= 8 mA operating at VGS=-1 V and a very small vDS, with the aid of Spice, determine the value of rDS.
5.10. Using Spice as a curve tracer, plot the iD - vDS characteristics of an n-channel JFET with IDSS=8 mA and VP=-4 V and lambda=0.01V-1. Provide curves for VGS=-5, -4, -3, -2 and 0 volts. Show the characteristics for vDS up to 10 V.
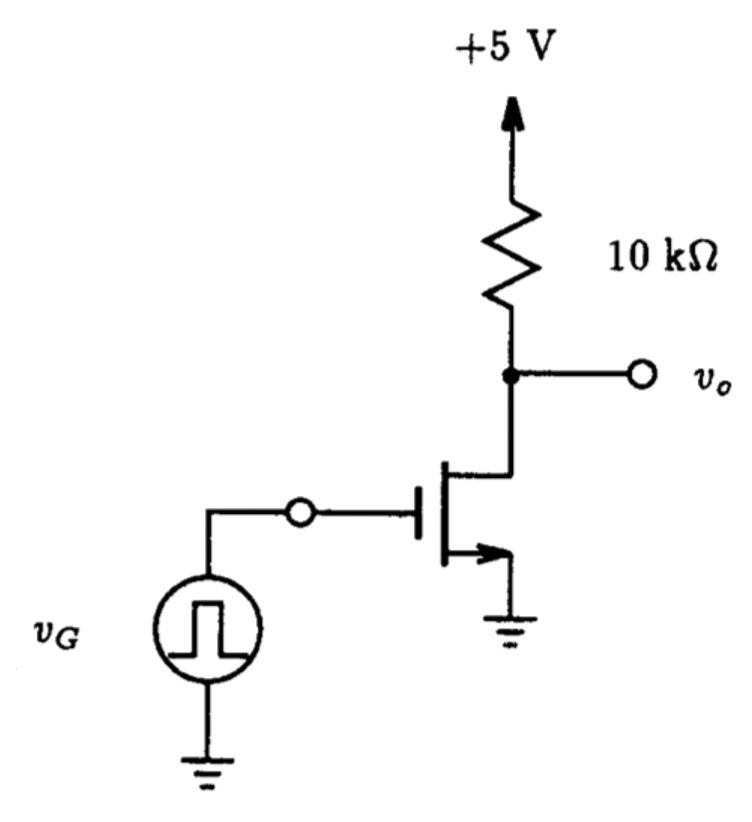
Fig. P5.11
5.11. The NMOS transistor in the circuit of Fig. P5.11 has Vt=1 V, uCOX= 1 mA/V2, and lambda=0.02 V-1. If vG is a pulse with 0 and 5 V levels and having a 1 ms pulse width, simulate the circuit using Spice and determine the pulse signal that appears at the output.
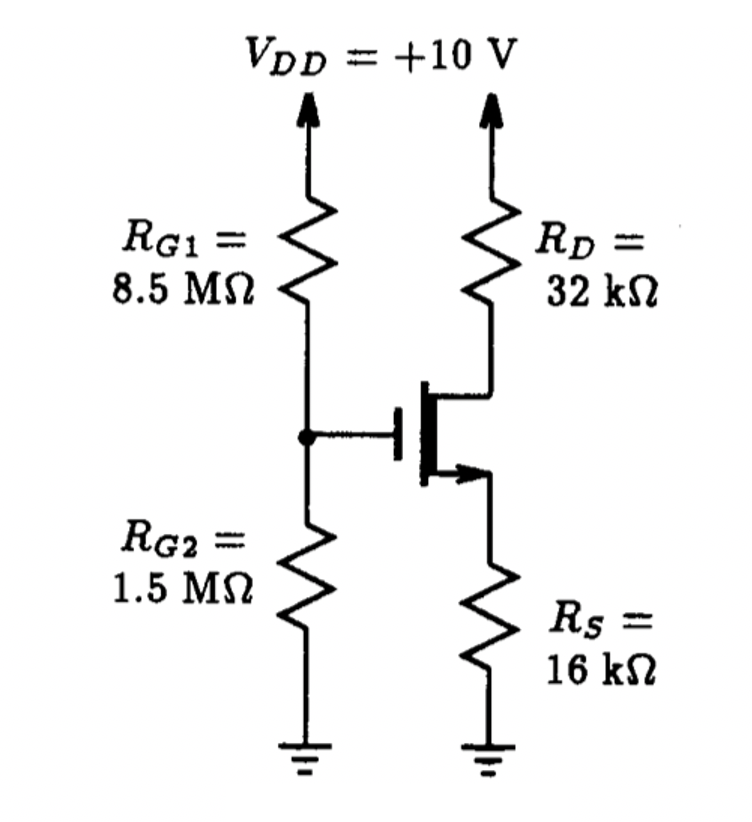
Fig. P5.12
5.12. Simulate the circuit in Fig. P5.12 to determine the drain current and the drain voltage. Assume that the depletion MOSFET has Vt=-1 V, uCOX= 1 mA/V2, and lambda=0.03 V-1. If K of the MOSFET increases by a factor of 2, determine the new level of drain current and drain voltage. Compare this to the previous case and note whether the biasing scheme is very effective.

Fig. P5.13
5.13. A MOSFET having uCOX= 2 mA/V2 and Vt=1 V operates in a feedback bias arrangement such as that shown in Fig. P5.13, from a 10 V supply with RD=8 kW and RG=10 MW. What value of ID results? If the FET is replaced by another with (a) uCOX= 1 mA/V2 and Vt=1 V, and (b) uCOX= 2 mA/V2 and Vt=2 V, what percentage change in ID results?
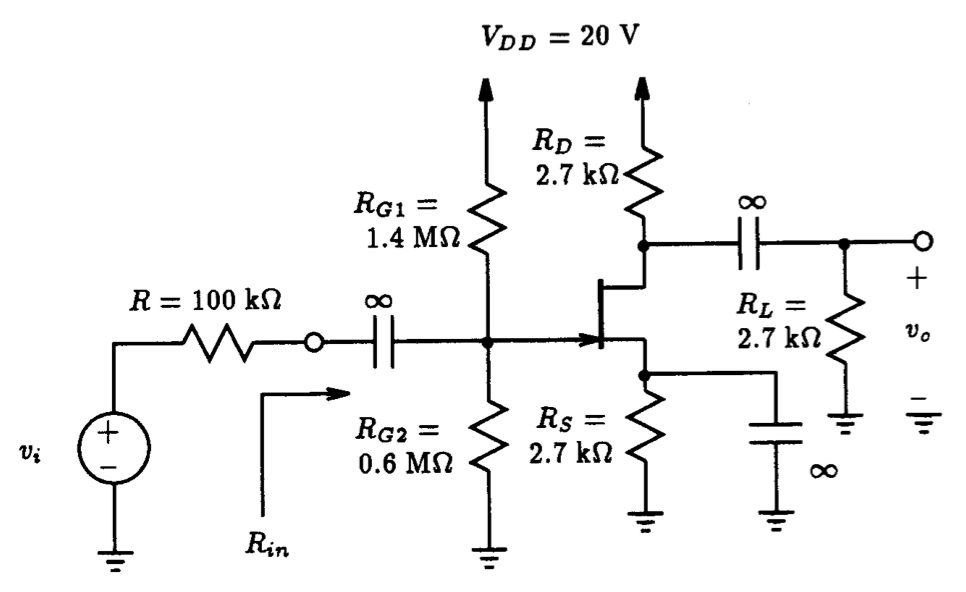
Fig. P5.14
5.14. The JFET in the amplifier circuit in Fig. P5.14 has VP=-4 V, IDSS=12 mA and lambda=0.003 V-1. Using Spice, answer the following:
(a) Determine the dc bias quantities V_G, ID, VGS, and vD associated with the JFET.
(b) Determine the overall voltage gain vo/vi and input resistance Rin.
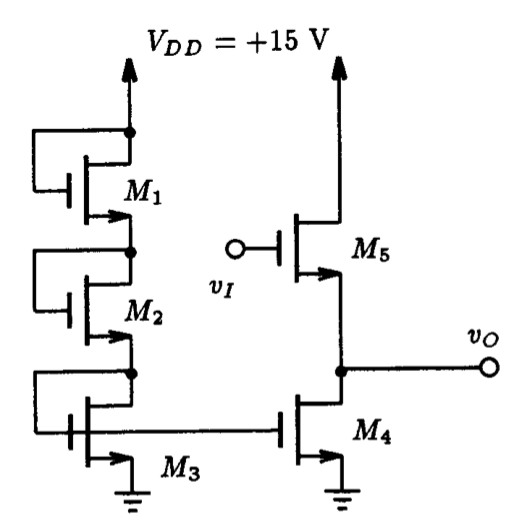
Fig. P5.15
5.15. In the circuit of Fig. P5.15 all devices are matched and assumed to have the following parameters: uCOX=50 uA/V2, W=L=25 um and Vt=2 V. Using Spice, plot the transfer characteristics vO vs. vI between VDD and ground. What is the small-signal voltage gain in the linear region of this amplifier? What is the corresponding output resistance?
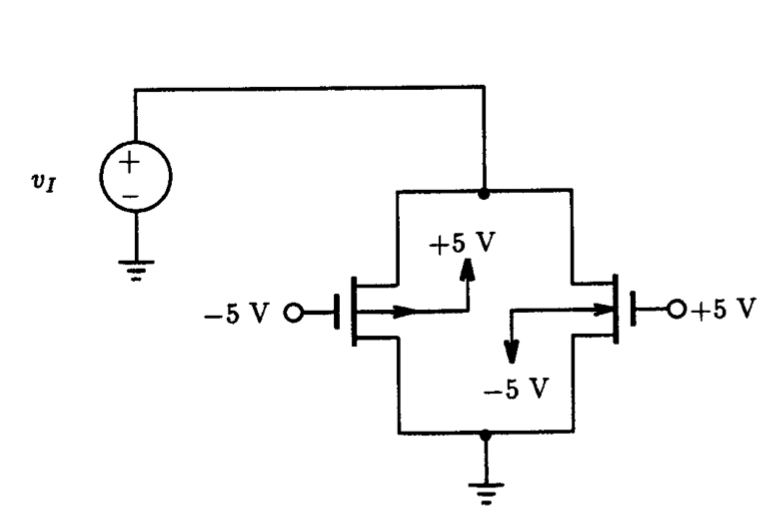
Fig. P5.16
5.16. A CMOS switch for which uCOX= 50 A/V2, g=0.3 V1/2 and |Vt0|=2 V is placed in the circuit setup shown in Fig. P5.16 for measuring its on-resistance. Sweep the input voltage signal vI from -5 V to +5 V using Spice and determine the resistance of the switch over this range of signals. Compare these results to those obtain from a switch consisting of a single n-channel MOSFET.
5.17. A CMOS switch is used to connect a sinusoidal source of 0.1 sin(2p 103t) to a load consisting of a 10 kW resistor and a 5 pF capacitor. If the control terminals of the switch are driven by complementary signals of ±5 V at a frequency of 10 kHz, simulate the transient behavior of the switch using Spice. Assume that the model parameters of the NMOS and PMOS devices are unCOX=20 A/V2, upCOX=10 A/V2, |Vt0|=1 V, g=0.3 V1/2, L_n=L_p=5 um, Wn=15 um, and Wp=30 um.
5.18. Using Spice as a curve tracer, plot the iD - vDS characteristics of an n-channel MESFET with b=10-4 A/V2, Vt=-1 V, IS=10-15 A and lambda=0.1 V-1. Provide curves for VGS=-5, -4, -3, -2 and 0 volts. Show the characteristics for vDS up to 10 V.
5.19. The n-channel MESFET in the circuit of Fig. 5.50 has Vt=-1 V, b=0.1 mA/V2, and lambda=0.1 V-1. If vi is a pulse with -5 and 0 V levels of 1 us pulse width, simulate the circuit using Spice and plot the pulse signal that appears at the output.